Deflection and Stiffness

4.10   Statically Indeterminate Problems

• A system is over-constrained when it has more unknown support reactions than static equilibrium equations.
• Such a system is said to be statically indeterminate and the extra reactions are called redundant reactions (redundant constraint support).
• To obtain a solution, a deflection equation is required for each redundant support reaction.

Shown are three support reactions and only two static equilibrium equations are available.
This beam has one redundant support. To solve for the three unknown support reactions we use the two equilibrium equations and one additional deflection equation.

 

Shown is a beam that has a wall on both ends, giving rise to two redundant supports requiring two deflection equations in addition to the equations from statics.

• The purpose of redundant supports is to provide safety and reduce deflection.

Nested helical springs Example:
When this assembly is loaded by the compressive force F, it deforms through the distance δ. What is the compressive force in each spring?
Only one equation of static equilibrium can be written. It is

Since there are two unknowns and only one static equilibrium equation, the system is statically indeterminate.
Deflection equation is: the two springs have the same deformation.

Or

Solve for F1 and sub. Into (a), we get

thus                

and                 
Thus, for two springs in parallel, the overall spring constant is k = F/δ = k1 + k2 .

• Next we will show two basic procedures for general statically indeterminate problems.

 

Procedure 1

• Choose the redundant reaction(s). May have alternative choices.
• Write the equations of static equilibrium for the remaining reactions in terms of the applied loads and the redundant reaction(s).
• Write the deflection equation(s) for the point(s) at the locations of the redundant reaction(s) in terms of the applied loads and the redundant reaction(s). Normally the deflection(s) is (are) zero. (may use superposition or strain energy).
• The equations from steps 2 and 3 can now be solved to determine the reactions.

Example 4-14 (see textbook)

Procedure 2 (omit)
Example 4-15 (see textbook) (omit)

 

4.11   Compression Members—General

• It is convenient to classify compression members according to their length and according to whether the loading is central or eccentric (long & short meterstick).
• Column – Straight, slender members loaded axially in compression such that either its length or eccentric loading causes it to experience more than pure compression.
• They are used in trusses and framework of buildings. Also used in machine linkages, sign posts, support for highway overpasses.
• Buckling is a sudden large lateral deflection of a column due to a small increase in an existing compressive load. This leads to instability and collapse of the member.
• Four categories of columns: (to help develop methods of analysis and design)
• Long columns with central loading
• Intermediate-length columns with central loading
• Columns with eccentric loading
• Struts or short columns with eccentric loading

4.12   Long Columns with Central Loading

• In the figure shown: (a) Both ends rounded or pivoted; (b) both ends fixed; (c) one end free and one end fixed; (d) one end rounded and pivoted, and one end fixed.
• If the axial force P acts along the centroidal axis of the column, simple compression of the member occurs for low values of the force.
• When P reaches a critical value, the column becomes unstable and bending develops rapidly (buckling).
• Critical load depends on end conditions.
• For pin-ended column (Fig. (a)), critical load is given by Euler column formula,

• It applies to apply to other end-conditions:

where the constant C depends on the end conditions as shown. In practice it is difficult, if not impossible, to fix the column ends so that values of C apply. Some designers never use a value of C greater than unity. However, if liberal factors of safety are employed, recommendations are summarized in Table shown.

 

 

 

 

 

• Using I = A k2, where A is the cross-sectional area and k is the radius of gyration, Euler column formula can be expressed as

where l/k is called the slenderness ratio,  used to classify columns according to length categories.
Pcr /A is the critical unit load, the load per unit area necessary to place the column in a condition of unstable equilibrium, where any slight movement of the support or load, will cause the column to begin to collapse (buckle). This is not a material property.

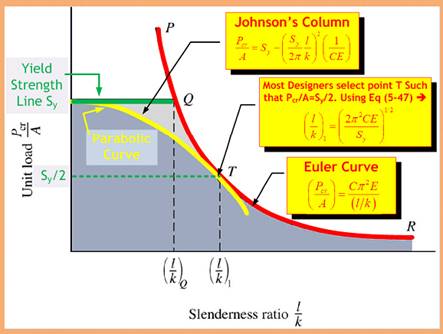
• Plotting Pcr /A vs l/k, with C = 1 gives the curve PQR shown.

Since the yield strength of the material has the same units as the unit load, the horizontal line through Sy and Q has been added to the figure.

• The designer will be aware of the end conditions and will attempt to configure the ends, using bolts, welds, or pins, for example, so as to achieve the required ideal end conditions. However, tests show numerous failures for columns with slenderness ratios below and in the vicinity of point Q, as shown in the shaded area of the figure.
• A column failure is always sudden, total, unexpected, and hence dangerous. There is no advance warning. A beam will bend and give visual warning that it is over loaded.
• For this reason neither simple compression methods nor the Euler column equation should be used when the slenderness ratio is near (l/k)Q. A conservative approach near Q is desired.
• Most designers select point T such that Pcr /A = Sy / 2. Using Eq. (4–44), we find the corresponding value of (l/k)1 to be

For (l/k) > (l/k)1, use Euler equation
For (l/k) ≤ (l/k)1, use a parabolic curve between Sy and T

4.13   Intermediate-Length Columns with Central Loading

• For intermediate-length columns, where (l/k) ≤ (l/k)1, use a parabolic curve between Sy and T.
• The parabolic or J. B. Johnson formula now seems to be the preferred one among designers in the machine, automotive, aircraft, and structural-steel construction fields.
• The general form of the parabolic formula is

• If parabola starts at Sy, then a = Sy
• If parabola fits tangent to Euler curve at T (Pcr /A = Sy/2), then

• Upon substituting in parabolic formula, also known as J.B. Johnson formula

4.14   Columns with Eccentric Loading

• For eccentrically loaded column with eccentricity e (as shown),

M = - P (e + y)

• Substituting into d2y / dx2 = M / EI,

 

• The solution of Eq. (a), for the boundary conditions y = 0 at x = 0 and  at x = l, is

 

• By substituting x = l/2 in Eq. (b) and using a trigonometric identity, we obtain

• The magnitude of the maximum bending moment also occurs at midspan and is

• The maximum compressive stress includes axial and bending

• Substituting Mmax from Eq. (4-48)

• Using the compressive yield strength Syc as the maximum value of σc, we can write Eq. (4–49) in the form

• This is called the secant column formula. The term (ec/k2) is called the eccentricity ratio.
• Equation (4–50) cannot be solved explicitly for the load P. Design charts, in the fashion of Fig. 4–21, can be prepared for a single material if much column design is to be done. Otherwise, a root-finding technique using numerical methods must be used.

• Figure shown is a plot of Eq. (4–50) for steel having compressive (and tensile) yield strength of 40 kpsi. Note how the P/A contours asymptotically approach the Euler curve as l/k increases.

           

 

Examples 4-16 to 4-19 (see textbook)

Euler Equation (4.44) for round cross sections:

Euler Equation (4.44) for rectangular cross sections:

J. B. Johnson Equation (4.46) for round cross sections:

J. B. Johnson Equation (4.46) for rectangular cross sections:

 

 

4.15   Struts or Short Compression Members (omit)

• A short bar loaded in pure compression by a force P along the centroidal axis will shorten in accordance with Hooke’s law, until the stress reaches the elastic limit. If the force P is increased, the material either becomes “barrel-like” or fractures.
• When there is eccentricity in the loading, the elastic limit is encountered at smaller loads.
• A strut is a short member loaded in compression, as shown.
• If eccentricity exists, maximum stress is at B (at a midway section) with axial compression and bending:

where k = (I/A)1/2 which is the radius of gyration, c is the coordinate of point B, and e is the eccentricity of loading.

• Note that the stress is not a function of length; how long is a short member?
• The difference between the secant formula Eq. (4–50) and Eq. (4–55) is that the secant equation accounts for an increased bending moment due to bending deflection. Thus the secant equation shows the eccentricity to be magnified by the bending deflection. This difference between the two formulas suggests that one way of differentiating between a “secant column” and a strut is to say that in a strut, the effect of bending deflection must be limited to a certain small percentage of the eccentricity.
• If bending deflection is limited to 1 percent of e, then from Eq. (4-44), the limiting slenderness ratio for strut is

This equation then gives the limiting slenderness ratio for using Eq. (4–55).
If the actual slenderness ratio is greater than (l/k)2, then use the secant formula; otherwise, use Eq. (4–55).

Examples 4-20 (see textbook) (omit)