Introduction
Evaporators and condensers are sensible heat exchangers in which one of the fluids, the refrigerant, changes phase. They are constructed similar to the sensible heat exchangers described in Chapter 13. An evaporator in a chilled water system would typically be a shell and tube exchanger with refrigerant contained in the shell and outside the tubes. Water would flow through the tubes and be cooled by the evaporation of the refrigerant. The liquid refrigerant from the condenser passes through the expansion valve and then enters the evaporator as a low temperature mixture of vapor and liquid. The vapor is usually slightly superheated before it leaves the evaporator and enters the compressor. Most of the heat transfer occurs during the change of phase.
Direct expansion coils (DX) are used in systems in which air is cooled and dehumidified. The refrigerant flows inside the tubes of the coil and evaporates while air flows over the surfaces. As this refrigerant stream passes through the coil, the liquid portion evaporates and the vapor fraction progressively increases so that the leaving stream is entirely vapor. In most DX coil applications the air is dehumidified. Direct expansion coils are common in appliances such as refrigerators, air-conditioners, and the air handlers found in typical HVAC distribution systems.
As with evaporators, there are two basic types of condensers. In water-cooled condensers, constructed as shell and tube exchangers, relatively cool water flows through the tubes. Refrigerant condenses on the outside of the tubes and then drains from the bottom of the exchanger. Air-cooled condensers are similar to cooling coils, with the refrigerant condensing inside tubes and transferring heat to the relatively cool air stream flowing over the outside of the tubes. In evaporative condensers liquid water is sprayed over the outside of the tubes and then evaporates into the air stream flowing over the tubes. The performance of these heat and mass exchangers is covered in Chapter SM 4.
The refrigerant typically enters a condenser from the compressor as superheated vapor. The vapor is cooled to saturation, condensed and then subcooled slightly. In the desuperheating section both the refrigerant and cooling fluid change in temperature, while during the phase change the temperature of the refrigerant is constant as it condenses. Although the majority of the heat transfer is from the refrigerant during the phase section, a significant portion does occur during de-superheating.
SM 7.2 Thermal Performance of Shell-and-Tube Evaporators
Flooded evaporators are common in chilled water circuits where heat is transferred from water flowing through tubes to a refrigerant evaporating on the outside of the tubes. A flooded shell and tube evaporator is shown in Figure 7.1. The tubes are relatively small diameter (1 inch or 2 cm) and closely spaced, and only a few tubes are shown in Figure 7.1.
Figure 7.1 Shell and tube flooded evaporator
The tubes are submerged in a pool of liquid refrigerant with a pump used to circulate the liquid refrigerant so that it continually flows over the heat transfer surfaces. In some applications the two-phase mixture leaving the expansion valve is separated into liquid and vapor components with only the liquid is sent to the evaporator. This reduces the flow through the evaporator. As the liquid evaporates the vapor leaves, usually with a small amount of superheat, and is sent to the compressor. The chilled water is then circulated to coils where it cools and dehumidifies and air stream.
Direct expansion evaporators are also used to cool liquids. The exchanger is a shell and tube type similar to that shown in Figure 7.1. However, in a direct expansion liquid evaporator the refrigerant is inside the tubes and evaporates as it flows.
Although the detailed fluid flow and heat transfer characteristics of these two types of evaporators are different, the same basic ideas apply. In the section where the refrigerant evaporates the refrigerant temperature is constant and the capacity rate ratio is zero. In the superheating section the refrigerant temperature changes and the capacitance rate ratio is finite. Different effectiveness relations would apply to these two sections. However, since most of the heat is transferred during the evaporation process, the approximation that C* is zero for the entire evaporator is usually sufficiently for the design or evaluation of an evaporator.
Example 7.1 illustrates the calculation of the performance of an evaporator and shows the degree of error in assuming that the capacitance rate ratio is zero throughout. Although this example is for a cooling a liquid the same ideas would apply for sensible cooling of an air or another gas stream.
"Example 7.1 An evaporator is used to chill a liquid water flow rate of 150 gpm that enters at 45 F. The refrigerant is a flow of 7550 lbm/hr of R-22 that enters at a quality of 0.1 and a temperature of 30 F. The evaporator has an overall heat transfer conductance of 60,000 Btu/hr-F. Determine heat transfer rate, the refrigerant outlet state, and the water outlet temperature."
"The performance will first be calculated assuming that the evaporator is a single heat exchanger with a capacitance rate ratio of zero. Then, the evaporator will be evaluated as two exchangers: an exchanger in which the refrigerant evaporates and one in which the refrigerant vapor is superheated. The relations in Section 7.3 will be used to find the thermal performance."
"Problem specifications"
T_w_i = 45 "F" "Temperature"
V_dot_w = 150 "gpm" "Volume flow rate"
T_r = 30 "F" "Temperature"
x_i = 0.1 "Quality"
m_dot_r = 7750 "lbm/hr" "Mass flow rate"
UA = 60000 "Btu/hr-F" "Overall UA"
"Refrigerant properties"
h_r_i = enthalpy(R22,T=T_r,x=x_i) "Btu/lbm" "Enthalpy"
p_r = pressure(R22,T=T_r,x=1) "psia" "Pressure"
"Water properties"
rho_f = density(water,T=T_w_i, x = 0) "lbm/ft3" "Density"
cp_f = specheat(water, T =T_w_i, x = 0) "Btu/lbm-F" "Specific heat"
m_dot_w = rho_f*V_dot_w*convert(gpm,ft^3/hr) "lbm/hr" "Mass flow rate"
C_w = m_dot_w*cp_f "Btu/hr-F" "Capacitance rate"
"The evaporator is analyzed as a single exchanger with C_star = 0 for entire exchanger. The effectiveness is taken from Table 13.1."
Ntu_0 =UA/C_w "Ntu"
epsilon_0 = 1-exp(-Ntu_0) "Effectiveness"
epsilon_0 = Q_0/Q_max_0 "Effectiveness"
Q_max_0 = C_w*(T_w_i - T_r) "Btu/hr" "Maximum heat flow"
"Energy balances are used to determine the outlet state of the water T_w_0_o and refrigerant h_r_0_o "
Q_0= C_w*(T_w_i - T_w_0_o) "Btu/hr" "Heat flow"
Q_0 = m_dot_r*(h_r_0_o - h_r_i) "Btu/hr" "Heat flow"
h_r_0_o = enthalpy(R22,T=T_r_0_o,p=p_r) "Btu/lbm" "Enthalpy"
Results
Treating the evaporator as a single heat exchanger results in a heat transfer rate of 620,100 Btu/hr. The refrigerant outlet temperature is 35.1 F, corresponding to 5.1F of superheat. The outlet water temperature is 36.8 F. These results will serve as a reference for the performance calculated assuming that the evaporator has two sections.
"The second performance calculations will treat the exchanger as two evaporators. The first section will be where the refrigerant evaporates and the second section will be where it is superheated."
"For the evaporating section the value of C_star is zero and the effectiveness is from Table 13.1. The overall conductance for this section will be expressed as UA_e = F*UA where F is the fraction of the UA in the evaporation section. At the end of this section the refrigerant is saturated vapor at 30 F and the enthalpy h_r_x at the end of this section is known (174.0 Btu/lbm).
The temperature of the water at the end of the evaporation section, T_w_x, is not known because the water has been cooled in the superheating section. As a result the performance of this section cannot be obtained directly. The solution for this section is coupled to that for the superheating section and obtained through iteration.
For the evaporation section:"
h_r_x = enthalpy(R22,T=T_r,x=1) "Btu/lbm" "Enthalpy"
Ntu_e = F*UA/C_w "Ntu"
epsilon_e = 1-exp(-Ntu_e) "Effectiveness"
epsilon_e = Q_e/Q_max_e "Effectiveness"
Q_max_e = C_w*(T_w_x - T_r) "Btu/hr" "Maximum heat flow"
Q_e = m_dot_r*(h_r_x - h_r_i) "Btu/hr" "Heat flow"
Q_e = C_w*(T_w_x - T_w_o) "Btu/hr" "Heat flow"
"For the superheating section the value of C_star is finite. The geometry is assumed to be counterflow and the effectiveness is from Table 13.1. The overall conductance of this exchanger is the remaining fraction of the entire exchanger, or UA_s = (1-F)*UA.
The unknown water temperature T_w_x couples the solution for the superheater to that for the evaporation section.
The capacitance rate of the refrigerant vapor is determined using the specific heat of the vapor and the mass flow rate, and the minimum capacitance is smaller of the water and refrigerant capacitance rates.
For the superheating section”
C_r_s = m_dot_r*cp_r "Btu/hr-F" "Capacitance rate"
cp_r = specheat(R22,T=T_r,x=1) "Btu/lbm-F" "Specific heat"
C_min_s = min(C_w,C_r_s) "Btu/hr-F" "Capacitance rate"
C_max_s = max(C_w,C_r_s) "Btu/hr-F" "Capacitance rate"
C_star_s =C_min_s/C_max_s "Capacitance rate ratio"
Ntu_s = (1-F)*UA/C_min_s "Ntu"
epsilon_s= (1-exp(-Ntu_s*(1-C_star_s)))/(1-C_star_s*exp(-Ntu_s*(1-C_star_s))) "Effectiveness"
epsilon_s = Q_s/Q_max_s "Effectiveness"
Q_max_s = C_min_s*(T_w_i - T_r) "Btu/hr" "Maximum heat flow"
Q_s = m_dot_r*(h_r_o_s - h_r_x) "Btu/hr" "Heat flow"
h_r_o_s = enthalpy(R22,T=T_r_o_s,p=p_r) "Btu/lbm" "Enthalpy"
Q_s = C_w*(T_w_i - T_w_x) "Btu/hr" "Heat flow"
"The total heat transfer equals the sum of the evaporation and superheat sections."
Q_ss = Q_e + Q_s "Btu/hr" "Heat flow"
Results and Discussion
For the superheating section the refrigerant has a capacitance rate of 1370 Btu/hr-F and it is the minimum capacitance rate. The capacitance rate ratio is 0.0182. Solving the set of equations simultaneously yields a fraction of the evaporating section of 0.9925. This shows that superheater section comprises only 0.75 percent of the surface area. The refrigerant and water outlet temperatures are 34.7 F and 36.8 F respectively. The refrigerant is superheated 4.7 F, which is only slightly less than the 5.1 F computed using the capacitance rate ratio of zero throughout.
SM 7.3 Thermal Performance of Direct Expansion Cooling Coils
In a direct expansion cooling coil, the refrigerant enters from the expansion valve as a low quality mixture of vapor and liquid. The liquid fraction evaporates during its passage through the coil and leaves at a slightly superheated condition. The temperature of the refrigerant is constant during the phase change process and, as discussed in Section 13.2, the capacitance of the refrigerant is infinite. Because the amount of superheat is small (5 – 10 F or 2- 5 C), a DX coil can be analyzed as an exchanger with a capacity rate ratio of zero.
On the air side of a DX coil there is usually both cooling and dehumidification. The design or analysis of a DX coil then brings in performance relations both for sensible heat exchanger and for heat and mass transfer. As discussed in Section 15.3, the performance of a cooling coil can be determined assuming two different conditions. The first is that the coil is completely wet and the second is that the coil is completely dry. The maximum of the heat transfer rates from these to determinations is quite close to the actual heat transfer rate for a coil that is partially wet. The analysis for the heat transfer only section can be treated using the sensible heat exchanger relations of Section 13.3 and illustrated for a shell and tube evaporator in Section 13.2. The analogy method for a chilled water coil was discussed in Section 15.4 and can be extended to a DX coil.
In a DX coil the refrigerant has an infinite sensible capacity rate, and by extension an infinite mass capacity rate. The parameter m* corresponds to the sensible capacity rate ratio C*, and is then zero for a DX coil. The Number of Transfer Units for mass transfer, Ntu*, is determined as presented in Section 13.6:
(7.1)
where U* is the overall mass transfer conductance based on the air-side area, Aa is the area on the air side, and 
is the air mass flow rate. The overall mass transfer conductance is given as
(7.2)
where cp is the specific heat of air, 
is the overall air-side surface efficiency for mass transfer, hc is the air-side convection coefficient, cs is the effective specific heat, Ur is the conductance on the refrigerant side, and Ar is the refrigerant-side area. The resistance of the surface separating the air and refrigerant is assumed negligible. The effective specific heat is estimated using a finite difference approximation around the temperature of refrigerant:
(7.3)
The effectiveness for the DX coil is then computed using the analogous relation for a sensible heat exchanger with a capacity rate ratio of zero
(7.4)
With the effectiveness, the heat transfer can be determined using the relation
(7.5)
where ha,in is the enthalpy of saturated air at the inlet conditions and hr, sat is the enthalpy of saturated air at the refrigerant temperature. The air outlet humidity ratio is then determined from an energy balance on the air flow
(7.6)
As with the chilled water coil, the analogy method yields only the outlet air enthalpy. The outlet temperature and humidity are determined using the relations presented in Section SM 2.2. Example 7.2 shows the determination of performance for DX coil.
"Example 7.2 Determine the performance of a DX coil. The air enters the coil at a dry bulb temperature of 75 F and a wet bulb temperature of 60 F with a volume flow rate of 5000 cfm. The refrigerant is R-22 at a temperature of 40 F that enters with a quality of 0.1 and leaves with 5 F superheat. On the airside the heat transfer conductance Ua is 50 Btu/hr-ft2 and the surface area is 360 ft2. On the waterside the heat transfer conductance Uw is 1000 Btu/hr-ft2 and the area is 18 ft2"
"Problem specifications
Air side”
p_atm = 14.7 "psia" "Atmospheric pressure"
T_a_i = 75 "F" "Dry-bulb temperature"
Twb_a_i = 60 "F" "Wet-bulb temperature"
V_dot_a = 5000 "cfm" "Volume flow rate"
“Refrigerant side”
T_r = 40 "F" "Refrigerant temperature"
DT_sh = 5 "F" "Temp. difference"
"Heat Exchanger Parameters"
U_a = 50 "Btu/hr-ft2-F" "Conductance"
A_a = 360 "ft2" "Area"
U_r = 1000"Btu/hr-ft2-F" "Conductance"
A_r = 18 "ft2" "Area"
"Air properties
Determine the properties of air, the mass flow rate, and the sensible capacitance rate for the air flow through the coil."
w_a_i = HumRat(AirH2O,T=T_a_i, p=p_atm,B=Twb_a_i ) "lbmw/lbma" "Humidity ratio"
h_a_i= Enthalpy(AirH2O,T=T_a_i,p=p_atm,B=Twb_a_i ) "Btu/lbm" "Enthalpy"
rho_a_i= density(AirH2O,T=T_a_i,p=p_atm,B=Twb_a_i ) "lbm/ft3" "Density"
m_dot_a = rho_a_i*V_dot_a*convert(1/min,1/hr) "lbm/hr" "Mass flow rate"
cp_a = SpecHeat(AirH2O,T=T_a_i,p=p_atm,B=Twb_a_i ) "Btu/lbm-F" "Specific heat"
C_a = m_dot_a*cp_a "Btu/hr-F" "Capacitance rate"
"The performance of the DX coil will be determined following the analogy approach of Section 13.6. It will be assumed first that the coil is completely wet and second that the coil is completely dry. The maximum of the two heat transfer rates approximates actual heat transfer rate for a coil that is partially wet. It will also be assumed that DX coil can be treated as a single exchanger with the capacitance rate of the refrigerant infinite. As shown in Example 7.1, because the amount of superheat is small this is a good assumption"
"In the analogy method the refrigerant is treated as an equivalent saturated air stream with an effective specific heat c_s. The enthalpy of saturated air at the refrigerant temperature is"
h_r_sat= Enthalpy(AirH2O,T=T_r,p=p_atm,R=1) "Btu/lbm" "Enthalpy"
"The effective specific heat c_s is aproximated using finite differences around the refrigerant temperature and a temperature increment of 2 F"
c_s = Dh_r/DT_r "Btu/lbm-F" "Specific heat"
Dh_r = Enthalpy(AirH2O,T=T_r+DT_r/2,p=p_atm,R=1)-Enthalpy(AirH2O,T=T_r-DT_r/2,p=p_atm,R=1) "Btu/lbm" "Enthalpy"
DT_r = 2 "F" "Temperature"
"Totally Wet Coil
The mass transfer resistances and the mass transfer Ntu_star are determined using the relations in Section 13.6 The overall surface efficiency is included the heat transfer conductance on the air side U_a "
U_star*A_a = 1/R_wet "lbm/hr" "Mass transfer cond."
R_wet = cp_a/(U_a*A_a) + c_s/(U_r*A_r) "hr/lbm" "Mass transfer resist."
Ntu_Star = U_star*A_a/m_dot_a "Mass transfer Ntu"
"The value of m* is zero and therefore the energy effectiveness for the totally wet coil is given by the expression for a sensible heat exchanger with C*=0 (Table 13.1)."
eff_wet = (1 - exp(-Ntu_Star)) "Wet coil effectiveness"
"The heat transfer and the air outlet enthalpy for the totally wet coil are determined using the expression for heat transfer in terms of effectiveness and an energy balance on the air side."
Q_dot_wet = eff_wet*m_dot_a*(h_a_i - h_r_sat) "Btu/hr" "Heat transfer rate"
Q_dot_wet =m_dot_a*(h_a_i- h_a_o) "Btu/hr" "Heat transfer rate"
"The analogy method directly determines the outlet air enthalpy. The air outlet temperature is determined using the approximation that the heat transfer is to a uniform temperature surface and the energy transfer is to a surface with a uniform enthalpy of saturated air that gives the actual heat transfer. The outlet temperature and enthalpy are used to determine the humidity ratio (Section SM 2.2)"
Ntu_a = U_a*A_a/(C_a)
h_s_eff = h_a_i +(h_a_o - h_a_i )/(1 - exp(-Ntu_a)) "Btu/lbm" "Enthalpy"
T_s_eff = Temperature(AirH2O,h=h_s_eff,p=p_atm,R=1) "F" "Temperature"
T_a_o = T_s_eff +(T_a_i - T_s_eff)*exp(-Ntu_a) "F" "Temperature"
w_a_o = Humrat(AirH2O,T=T_a_o,p=p_atm,h=h_a_o) "lbmw/lbma" "Humidity ratio"
"The rate of condensation is determined from a mass balance on the air stream"
m_dot_cond = m_dot_a*(w_a_i - w_a_o) "lbm/hr" "Condensate flow rate"
“Results
For the totally wet coil assumption, the Ntu is 1.158, the effectiveness is 0.686, and the heat transfer rate is 167,719 Btu/hr. The condensation rate is 19.0 lbm/hr.”
"The heat transfer for a totally dry coil is determined using the relations for a sensible heat exchanger with a capacitance rate ratio of zero. The heat transfer resistances and the Ntu_dry are determined."
U_a_dry*A_a = 1/R_dry "Btu/hr-F" "Heat transfer cond."
R_dry = 1/(U_a*A_a)+1/(U_r*A_r) "hr-F/Btu" "Heat transfer resist."
Ntu_dry = U_a_dry*A_a/C_a "Heat transfer Ntu"
"The effectiveness for C* = 0 is (Table 13.1)"
eff_dry = (1 - exp(-Ntu_dry)) "Dry coil effectiveness."
"The heat transfer and the air outlet temperature for the totally dry coil are determined from the expression for effectiveness and an energy balance on the air stream."
Q_dot_dry = eff_dry*C_a*(T_a_i - T_r) "Btu/hr" "Heat transfer rate"
Q_dot_dry =C_a*(T_a_i- T_a_o_dry) "Btu/hr" "Heat transfer rate"
"The higher of the totally wet or totally dry calculation is determined and used to approximate the actual heat transfer."
Q_dot_coil = max(Q_dot_wet, Q_dot_dry) "Btu/hr" "Heat transfer rate"
“Results
For the totally dry coil assumption, the Ntu is 1.678, the effectiveness is 0.813, and the heat transfer rate is 152,654 Btu/hr. The heat transfer for the totally dry assumption is lower than that for the totally wet assumption and the totally wet calculation is closer to the actual heat transfer.”
"The refrigerant entering and exiting enthalpies are determined from the entering condition of a quality of 0.1 and an outlet condition of 5 F superheat. The refrigerant mass flow rate is determined from an energy balance on the refrigerant.”
h_r_i = enthalpy(R22,T = T_r, x = 0.1) "Btu/lbm" "Enthalpy"
p_r = pressure(R22,T = T_r, x = 0.1) "psia" "Pressure"
h_r_o= enthalpy(R22,T = T_r+DT_sh,p=p_r) "Btu/lbm" "Enthalpy"
Q_dot_coil = m_dot_r*(h_r_o - h_r_i) "Btu/hr" "Heat transfer rate"
“Results and Discussion
Even though the Ntu and effectiveness are larger for the totally dry assumption than for the totally wet coil assumption, the heat transfer rate is less. The maximum sensible heat transfer 
is less than the maximum latent transfer rate 
. Because the wet coil assumption yields the higher heat transfer rate it is closer to the partially wet coil case, and is taken as the coil heat transfer (Section SM 2.2)
SM 7.4 Heat Transfer Coefficients for Evaporators
The heat transfer coefficients for evaporation are different than the conventional convection relations described in Chapter 4. The process by which the refrigerant changes from liquid to vapor is a combination of boiling and evaporation, although a clear distinction between the two is usually not made. For both mechanisms, the surface temperature is higher than the saturation temperature. In boiling, vapor is produced at the solid surface and bubbles up through the liquid to the surrounding vapor, while in evaporation the liquid changes phase at the interface between the liquid and the vapor.
There are different types of evaporators with different geometries for the heat transfer process. In flooded evaporators, which are common in chilled water systems, refrigerant evaporates from the outside of tubes that are submerged in a pool of refrigerant and is collected at the top of the evaporator. Water or another heat transfer fluid flows on the inside of the tubes. In the direct expansion (DX) coils common in air systems, warm air flows over the outside of the tubes and evaporation of the refrigerant takes place inside the tubes.
The process of evaporation on the outside of tubes is often described as nucleate pool boiling. The term pool boiling refers to boiling from the hot tubes submerged in a pool of liquid, and nucleate refers to the boiling regime in which steady streams of small vapor bubbles are produced along the tubes. The bubbles rise to the surface of the refrigerant agitating the fluid and allowing cold liquid to flow to the tube surface and evaporate. The phase change occurs where the liquid is in contact with the surface, yielding high transfer rates.
Film boiling occurs when the tubes are so hot that all of the liquid at the surface boils and a layer of vapor forms around the tubes. The phase change occurs at the interface between vapor and liquid away from the tube surface. Heat is transferred from the tube surface by radiation and conduction through the vapor layer to the interface. The thermal resistance of the vapor layer is high and the heat transfer coefficients for film boiling are much lower than for nucleate boiling. In film boiling, the temperature differences between the fluid and surface are several of orders of magnitude higher than for nucleate boiling, which would be detrimental to the performance of a refrigeration system. Evaporators are therefore designed so that nucleate boiling occurs.
No really universal method is available to correlate and predict boiling heat transfer coefficients. The actual fluid temperature has little effect on the heat transfer, and the proposed equations can all be put in a form that relates the heat transfer coefficient to the difference between the surface temperature and saturation temperature of the fluid at that pressure. The correlations reduce to the basic form:
(7.7)
where Ts is the surface temperature and Tsat is the saturation temperature of the refrigerant. The proportionality constant C is a function of fluid thermodynamic and transport properties, including surface tension, and the characteristics of the surface, such as the roughness. The exponent n is about 3, but also depends on the fluid properties and surface characteristics. One of the earliest correlations that contains the relevant fluid properties is (Handbook of Phase Change: Boiling and Condensation, 1999):
(7.8)
where 
is the average heat flux, mf is the liquid viscosity, hfg is the latent heat of vaporization, Cs is an empirically determined coefficient, g is the acceleration due to gravity, s is the surface tension for the fluid, rf and rg are the densities of the liquid and vapor phases, Ts is the surface temperature and Tsat is the saturation temperature at the fluid pressure, cp,f is the specific heat of the liquid, kf is the thermal conductivity of the liquid. The correlation is in terms of the heat flux rather than a heat transfer coefficient since the flux is not linearly proportional to a temperature difference.
On the right-hand side are a number of non-dimensional groups of properties. In the first term in brackets, the difference in density between liquid and vapor multiplied by gravity reflects the buoyancy force that allows the bubbles to rise, and indicates that evaporation is a natural convection phenomenon. The liquid surface tension (s) relates to the force that is necessary for vapor bubbles to form in the liquid phase.
The relevant temperature difference is contained in the second term in brackets. Fluid and surface temperatures are equal at a surface. If the surface temperature is higher than the saturation temperature, boiling will occur at the surface independent of the bulk fluid temperature. The relevant driving force is then the difference between the surface and saturation temperatures. The specific heat times the temperature difference represents the energy required to heat the liquid and the latent heat of vaporization reflects the energy required to change phase. The last term in brackets is the liquid Prandtl number, which is an important fluid properties group.
The constant Cs is empirically determined. It is a strong function of surface conditions such as roughness, the surface composition such the type of metal, and the refrigerant. Equation 7.2 is useful for estimating the heat transfer when the constant Cs has been established. The original correlation was developed for non-refrigerants.
A more recent correlation was developed by Gorenflo (1993) (ASHRAE Handbook of Fundamentals, Chapter 4, 2005). The correlation was developed for a reduced pressure (the ratio of the pressure to the critical pressure for the fluid) of 0.1 and specified reference conditions. The correlation is
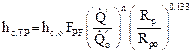(7.9)
where hc,TP is the heat transfer coefficient for two-phase boiling, hc,o is a reference value for the heat transfer coefficient that depends on the fluid, 
is a reference heat flux, n is an exponent that depends on the reduced pressure, Rp is the surface roughness, and Rpo is a reference roughness. The coefficient FPF is a correlated function of the reduced pressure.
Equations 7.8 and 7.9 can only approximate the heat transfer coefficients for evaporators. One reason is that the evaporation of the refrigerant can produce strong convection currents that augment the natural convection flow significantly. Another is that the flow over the tubes is very non-uniform and the coefficients are not equal throughout the evaporator. Equation 7.9 is useful, though, for extending measurements on a given evaporator under one condition to another condition.
Boiling inside tubes is more complicated than the boiling on the outside. The fluid enters a tube as a liquid and, as it is heated, becomes a saturated mixture of liquid and vapor. The evaporation process and flow regimes are shown schematically in Figure 7.2.
Figure 7.2 Flow regimes during evaporation or boiling
Initially, there is nucleate boiling at the wall that creates small bubbles that flow through the liquid layer to the core. Large bubbles of vapor then form in the core that grow and move along with the flow. Eventually, these large vapor bubbles coalesce and form a continuous core of vapor with the liquid flowing in an annular film along the wall. At high values of the mass flux, the annular flow pattern occurs over most of the tube length, whereas at low values the flow may become stratified with liquid moving along the bottom of the tube and vapor along the top. As the flow progresses down the tube, the liquid film on the walls becomes thinner and eventually disappears as all of the liquid evaporates.
There are two interacting mechanisms for boiling inside tubes. Forced convection dominates when the flow rates are high. Heat is transferred from the wall to the flowing liquid and evaporation occurs at the liquid vapor interface. The second mechanism is nucleate boiling at the wall surface, and this mechanism dominates when the heat flux is high or flow rate is low. The relations for heat transfer over the entire boiling range are based on a combination of these two mechanisms.
A correlation for the heat transfer coefficient for evaporation/boiling in tubes has been developed to predict the ratio of the two-phase heat transfer coefficient to that for a single-phase liquid flow (Kandlikar, Shoji, and Dhir, 1999). This ratio depends on the relative magnitudes of the flow rate and heat flux, and can be represented in terms of two non-dimensional parameters. One is the ratio of the density of the liquid phase to that of the vapor phase (rf/rg = r*). The second parameter is a “boiling number” 
that is defined in terms of the wall heat flux, refrigerant mass flux, latent heat of vaporization, and a surface parameter FFl:
(7.10)
where G is the mass flux (mass flow rate per unit cross sectional area). The fluid-surface parameter FFL reflects the interaction of the fluid and the surface, and depends on the specific refrigerant and the tube material. Values for FFl for refrigerants flowing inside copper tubes are given in Table 7.1. For stainless steel tubes the value of FFl is unity.
Table 7.1 Values of FFL for copper tubes.
Refrigerant |
FFL |
Refrigerant |
FFL |
R-11 |
1.30 |
R-113 |
1.30 |
R-12 |
1.50 |
R-114 |
1.24 |
R-13B4 |
1.31 |
R-134a |
1.63 |
R-22 |
2.30 |
R-152 |
1.10 |
From Chapter 15, Handbook of Phase Change: Boiling and Condensation, 1999.
The ratio of the heat transfer coefficient for two-phase (hTP) to that for single phase (hSP) is plotted in Figure 7.3 as a function of vapor quality for different values of the modified boiling number and the ratio of the liquid and vapor densities. The three curves for r* of 10, 100, and 1000 for a Bo* of 0.0001 are indicated at the left of Figure 7.3, and the corresponding curves for Bo* of 0.oo1 are indicated on the right. The local two-phase heat transfer coefficient varies with distance along the tube in that it depends on the local value of the quality, and it needs to be integrated over the tube length to compute the heat transfer.
It can be seen that the two-phase heat transfer coefficient can be up to twenty times larger than that for a single-phase liquid flow. The coefficient is highest for situations in which the liquid density is much larger than the vapor density (large values of r* = rf/rg). The two-phase heat transfer coefficient is also larger when the boiling number is large, which occurs with large heat fluxes or low mass flow rates. At a high value of the mass fraction of the vapor phase (high value of quality) the heat transfer coefficient is high when the vapor phase is much less dense than the liquid phase, but otherwise, quality has a relatively small effect.
Figure 7.3 Boiling heat transfer coefficients as a function of vapor quality.
Correlations have been developed for the curves shown on Figure 7.3 and are available in Kandlikar, Shoji, and Dhir (1999). Example 7.2 illustrates the use of this map in determining the heat transfer coefficient.
"Example 7.3 Determine the boiling heat flux and heat transfer coefficient inside the 0.5-inch diameter tubes of a DX coil at a location where the quality is 0.5. The refrigerant is R-22, the saturation temperature is 35 F, the wall temperature is 45 F, the tubes are copper, and the mass flow rate through each tube is 100 lb/hr."
“Problem specifications”
T_sat = 35 "F" "Temperature"
T_w = 45 "F" "Temperature"
x=0.5 "Quality"
D = 0.5*convert(in,ft) "ft" "Tube diameter"
m_dot = 100 "lbm/hr" "Mass flow rate"
"Surface finish factor for copper tubes (Table 7.1)"
F_Fl = 2.3 "Surface finish factor"
"Determine the liquid and vapor properties of the refrigerant "
rho_f = density(R22,x=0, T=T_sat) "lbm/ft3" "Density"
rho_g = density(R22,x=1, T=T_sat) "lbm/ft3" "Density"
h_f = Enthalpy(R22,x=0, T=T_sat) "Btu/lbm" "Enthalpy"
h_g = Enthalpy(R22, x=1, T=T_sat) "Btu/lbm" "Enthalpy"
h_fg = h_g - h_f "Btu/lbm" "Enthalpy"
mu_f = Viscosity(R22, x=0, T=T_sat) "lbm/hr-ft" "Viscosity"
k_f = Conductivity(R22,x=0, T=T_sat) "Btu/hr-ft-F" "Thermal conductivity"
Pr = Prandtl(R22,x=0, T=T_sat) "Prandtl number"
"Determine the single phase heat transfer coefficient using an appropriate relation from Table 4.3 in Section 4.3. A simple relation is used because the evaluation of the boiling coefficient is not that precise. “
N_u = 0.023*Re^0.8*Pr^0.4 "Nusselt number"
Re = 4*m_dot/(Pi*D*mu_f) "Reynolds number"
N_u = h_SP*D/k_f "Nusselt number"
“Results
The Reynolds for a single phase flow of liquid refrigerant is 6286. The flow is turbulent and with a Prandtl number of 2.52 the heat transfer coefficient is found to be 47.4 Btu/hr-ft2-F. The value of the heat transfer coefficient will be the base for determining the boiling heat transfer coefficient.”
"The calculation for the two phase heat transfer coefficient uses the correlation presented in Figure 7.3. The ratio of the liquid to vapor density rho_star is determined. The mass flux G is used in calculating the modified boiling number Bo_star. The boiling number depends on the heat flux which is not known at the start of the solution. The equation set is solved simultaneously with an estimate of the ratio of two-phase to single-phase heat transfer coefficients alpha from Figure 7.3 to find the modified boiling number, and then iterated until convergence is obtained. Surface finish factor for copper tubes is from Table 7.1"
rho_star = rho_f/rho_g "Density ratio"
G = m_dot/(Pi*D^2/4) "lbm/hr-ft2" "Mass flux"
Bo_star = (q``/(h_fg*G))*F_Fl^(1/0.7) "Boiling number"
alpha = 7 "h_TP/h_SP"
h_TP=alpha*h_SP "Btu/hr-ft2-F" "Two-phase coefficient"
q`` = h_TP*(T_w - T_sat) "Btu/hr-ft2" "Two-phase heat flux"
Results and Discussion
SM 7.5 Thermal Performance of Condensers
Condensers in air conditioning and refrigeration systems are air-cooled, water-cooled, or evaporatively cooled. Water-cooled condensers are generally shell and tube exchangers and are very similar to a chilled water evaporator. A two-pass water cooled condenser is shown schematically in Figure 7.4. Refrigerant vapor leaving the compressor enters at the top of the shell and flows downward. The vapor condenses on the outside of the tubes and drains by gravity out the bottom.
Air-cooled condensers are constructed similar to cooling coils, and, similar to water-cooled condensers, refrigerant vapor enters at the top and liquid refrigerant leaves at the bottom. In an air-cooled condenser the refrigerant is condensed inside tubes and air flows over the outside. Evaporative condensers, discussed in Chapter SM 4, are constructed similar to coils, but use evaporation of water from the heat transfer surfaces and into the air stream to condense the refrigerant.
Figure 7.4 Schematic of a water-cooled condenser
The refrigerant enters the condenser from the compressor, usually with a significant amount of superheat. The refrigerant vapor is cooled in the upper section of the condenser to the saturation temperature before condensation occurs. The heat transfer from the superheated vapor is in the range of 10 to 30 percent of the total heat transfer. The condensed refrigerant leaves at the bottom of the condenser. There is some subcooling by the lowest incoming water but the amount of heat transfer is much less than that for desuperheating.
In the condensing section the specific heat of the condensing fluid is infinite since the enthalpy changes without a corresponding temperature change. In this section the condensing fluid has an infinite capacitance rate and the capacitance rate ratio (C*) is zero. In the sections in which desuperheating and subcooling occur the capacitance rate ratio has a finite value. However, since most of the heat is transferred during the condensation process, the approximation that C* is essentially zero for the entire condenser is usually sufficiently accurate for design or evaluation. The condensing temperature is then used as the inlet temperature in determining the effectiveness.
In some circumstances it might be desirable to separately analyze the desuperheating and subcooling sections. The heat transfer coefficients on the refrigerant side are quite different in these sections. The heat transfer coefficient for the vapor in the desuperheating section is low and that for the subcooling section is high, although less than that for section in which condensation occurs. An accurate determination of the performance would involve dividing the exchanger up into three separate, but coupled exchangers. Each would have a different value for the number of transfer units and capacitance rate ratio. The solution would involve interation to find the outlet conditions. Example 7.3 illustrates the contribution that the desuperheating and subcooling sections make to the overall heat transfer in a condenser.
"Example 7.4 A water-cooled condenser is to be designed for a flow of 0.2 kg/s of R-22 that enters at a temperature of 125 C and a pressure of 1200 kPa and leaves at 25 C. The water enters at a temperature of 17 C and has a temperature rise of 10 C. Determine the required overall heat transfer coefficient for the condenser."
“Problem specifications”
m_dot_r = 0.2 “kg/s” “Mass flow rate”
p_sat = 1200 “kPa” “Pressure”
T_r_i = 125 “C” “Temperature”
T_r_o = 25 “C” “Temperature”
T_w_i = 17 “C” “Temperature”
T_w_o = 27 “C” “Temperature”
"Refrigerant properties"
T_sat = temperature(R22, p = p_sat, x = 1) “C” “Temperature”
h_g = enthalpy(R22, p = p_sat, x=1) “kJ/kg” “Enthalpy”
h_f = enthalpy(R22, p = p_sat, x=0) “kJ/kg” “Enthalpy”
h_fg = h_g - h_f “kJ/kg” “Enthalpy”
h_r_i = enthalpy(R22, p = p_sat, T = T_r_i) “kJ/kg” “Enthalpy”
h_r_o = enthalpy(R22, p = p_sat, T =T_r_o) “kJ/kg” “Enthalpy”
"The heat flow rate is determined from an energy balance using the refrigerant flow and enthalpy change"
q = m_dot_r*(h_r_i - h_r_o) “kW” “Heat flow rate”
"Water properties"
cp_w = specheat(water,T=T_w_i, x=0) “kJ/kg-C” “Specific heat”
"An energy balance on condenser that relates the heat transfer from the refrigerant to the evaporator is performed. This yields the water flow rate needed to condense the refrigerant and the corresponding capacitance rate"
q = m_dot_w*cp_w*(T_w_o - T_w_i) “kW” “Heat flow rate”
C_w = m_dot_w*cp_w “kW/C” “Capacitance rate”
"The condenser is first treated as a single heat exchanger. The effectiveness is determined from the ratio of the heat transfer to the water to the maximum heat transfer and then equated to the effectiveness relation for a C* of zero with the water flow as the minimum capacitance fluid. The resulting Ntu is then used to find the UA_s for the single heat exchanger approximation. "
epsilon = C_w*(T_w_o - T_w_i)/(C_w*(T_sat - T_w_i)) “Effectiveness”
epsilon = 1 - exp(-Ntu) “Effectiveness”
"The overall heat transfer coefficient for a single heat exchanger"
Ntu = UA_s/C_w “Ntu”
Results
The heat transfer based on the refrigerant mass flow rate and enthalpy difference is 52.4 kW, yielding a required water flow rate for the 10 C rise of 1.252 kg/s.
In treating the condenser as a single exchanger with a capacitance rate ratio of unity, it is assumed that all of the heat is transferred from the refrigerant at the constant saturation temperature of 30.25 C. The effectiveness for this assumption is 0.755, yielding an Ntu of 1.406 and a UA of 7.37 kW/C. This result will be compared to the more realistic design using two exchangers.
"The condenser is treated as being composed of two heat exchangers. One is the desuperheater (ds) and the other is the condenser and subcooler (cond). The solution is iterative in that the water temperature entering the desuperheater is unknown. For the desuperheater, the refrigerant leaves as saturated vapor. The heat flow is determined from the refrigerant mass flow rate and enthalpy difference."
q_ds = m_dot_r*(h_r_i - h_g) “kW” “Heat flow rate”
cp_r = (h_r_i - h_g)/(T_r_i - T_sat) “kJ/kg-C” “Specific heat”
"The desuperheater is a sensible heat exchanger with a finite capacitance rate ratio"
C_r = m_dot_r*cp_r“kW/C” “Capacitance rate”
C_star = C_r/C_w “Capacity rate ratio”
"The effectiveness of the desuperheater is based on the refrigerant as the minimum capacitance fluid. The water temperature entering the desuperheater T_w_ds is unknown. The effectiveness relation for a counter flow exchanger from Table 13.1 is used. The overall heat transfer coefficient for the desuperheater is determined from the Ntu."
epsilon_ds = q_ds/(C_r*(T_r_i - T_w_ds)) “Effectiveness”
epsilon_ds = (1 - exp(-Ntu_ds*(1-C_star)))/(1 - C_star*exp(-Ntu_ds*(1-C_star))) “Effectiveness”
Ntu_ds = UA_ds/C_r “Ntu”
"For the condenser and subcooler, the heat flow for the condensing and subcooling sections is based on the refrigerant mass flow rate and enthalpy difference. The heat flow to the water is used to find the temperature of the water entering the desuperheater."
q_cond = m_dot_r*(h_g - h_r_o) “kW” “Heat flow rate”
q_cond = C_w*(T_w_ds - T_w_i) “kW” “Heat flow rate”
"The effectiveness is based on the heat flow to the water and the water as the minimum capacitance fluid. The effectiveness for the condenser and subcooler is for a C* = 0 exchanger. The overall heat transfer coefficient is determined from the Ntu.”
epsilon_cond = q_cond/(C_w*(T_sat - T_w_i)) “Effectiveness”
epsilon_cond = 1 - exp(-Ntu_cond) “Effectiveness”
Ntu_cond = UA_cond/C_w “Ntu”
"The total overall transfer coefficient for the treatment of the condenser as two exchangers is the sum of that for the condenser and desuperheater."
UA_overall = UA_cond + UA_ds “kW/C” “Overall UA”
"The relative heat transfer rates for the single heat exchanger and for the two exchanger analysis are indicated by the relative temperature differences."
Deltah_single = h_r_i - h_r_o “kJ/kg” “Enthalpy”
Deltah_ds = h_r_i - h_g “kJ/kg” “Enthalpy”
Deltah_cond = h_g- h_f “kJ/kg” “Enthalpy”
Deltah_sc = h_f - h_r_o “kJ/kg” “Enthalpy”
Results and Discussion:
For the design treating the condenser as a single exchanger the heat transfer rate is 62.4 kW and the overall thermal conductance is 7.37 kW/C. The heat transfer rate is the same for both treatments.
For condensing/subcooling section the heat transfer rate is 36.8 kW. The water temperature increases from 17 C to 24.0 C in this section. The capacitance rate ratio C* is zero and the effectiveness is 0.531, yielding an Ntu_cond of 0.757 and a UA_cond of 3.96 kW/C.
For the desuperheater section the heat transfer rate is 15.6 kW. The capacitance rate of the refrigerant is 0.164 kW/C, and for the desuperheater the refrigerant capacitance rate is the minimum. For this sensible heat exchanger the effectiveness is 0.938, the Ntu is 2.85, and the UA is 0.47 kW/C.
The overall heat transfer coefficient for the two-exchanger design is the sum of the component UA values, or 4.43 kW/C. This value is significantly less than the 7.37 kW/C determined assuming that all of the heat was transferred at the saturation temperature. The assumption that the condenser can be treated as a single exchanger with a capacitance rate ratio of zero does not account for the fact that the vapor enters at a high temperature. The large temperature difference in the desuperheater means that the UA needs to be smaller. For the conditions of this condenser it is necessary to design the unit as two exchangers.
The enthalpy changes of the refrigerant in the heat exchanger for the three processes indicate the relative heat transfer:
Desuperheating to saturation vapor: 77.8 kJ/kg
Condensation at saturation: 176.3 kJ/kg
Subcooling from saturated liquid; 7.9 kJ/kg
Total enthalpy change 262 kJ/kg
SM 7.6 Heat Transfer Coefficients for Condensers
When refrigerant vapor comes into contact with a surface that is at a temperature below the dew point, vapor starts to condense. The condensing liquid is heavier than the vapor and flows downward under the influence of gravity. Depending on the condition of the surface on which the condensation occurs, the process may be either dropwise or filmwise condensation. In dropwise condensation, drops of condensate form on the surface and flow downward, leaving the surface essentially bare except for the areas on which the drops are forming. The rates of heat transfer are high since most of the condensing vapor is in intimate contact with the surface. In filmwise condensation, a film of condensate forms that covers the surface and continually drains. Condensation takes place at the film-vapor interface and the heat of condensation is transferred through the liquid film to the surface. The heat transfer rates for filmwise condensation are less than those for dropwise condensation due to the added thermal resistance of the condensate film. It is difficult to maintain a surface so that the drops do not coalesce and thus filmwise condensation usually occurs.
Condensation can occur on either the outside or the inside of the tubes of a refrigerant condenser, as shown schematically in Figure 7.5. In most water-cooled condensers the refrigerant condenses on the outside of the tubes. The condensate drips from the tubes and is removed from the shell of the condenser at the bottom. In air-cooled condensers, the refrigerant flows inside the tubes and condensate drains from the tube at the condenser headers. Although the geometries are quite different the mechanisms are similar and the same fluid properties govern the heat transfer.
Figure 7.5 Condensation on the outside and inside of tubes
For the relatively small diameter tubes found in refrigeration condensers the condensate flow on the outside of tubes is laminar rather than turbulent, and only the laminar relations will be presented. The laminar heat transfer coefficient for condensation on the outside of a horizontal tube can be represented by equation 7.11, and is often termed a “falling film” correlation. The important parameter is the density difference between the liquid and vapor that creates the buoyancy force that causes the fluid to flow, similar to that for natural convection. The term inside the brackets is analogous to a Rayleigh number and the exponent on the grouping of properties is 0.25, which is the same as for laminar natural convection. The Nusselt number based on the tube diameter D is given by:
(7.11)
where kf is the liquid thermal conductivity, g the acceleration due to gravity, rf and rg are the liquid and vapor densities, respectively, mf is the liquid viscosity, Tsat and Ts are the saturation and surface temperature, respectively. The term 
is a modified heat of vaporization that includes the thermal effect of subcooling the vapor from the saturation temperature to the surface temperature, and is given by:
(7.12)
where hfg is the heat of vaporization at the saturation temperature and cp,f is the specific heat of the liquid. The film of condensate on a tube is quite thin, and is determined as:
(7.13)
These relations include the important properties that govern condensation heat transfer. The downward flow of the condensate is driven by gravity. With an increasing difference the film thickness is thinner and the heat transfer coefficient higher. Increased viscosity results in a thicker film and less heat transfer. Increased conductivity, which is in both the Nusselt number definition and the correlation parameter, increases the heat transfer coefficient. An increased latent heat of vaporization increases the heat transfer per unit mass, and results in an increased coefficient. An increased difference between the surface and saturation temperatures increases the film thickness since the rate of condensation is increased, which reduces the heat transfer coefficient. The heat flow, though, which is the product of the heat transfer coefficient and the temperature difference between the fluid and surface, increases. Equation 7.11 has been found to underpredict the heat transfer by 15 to 20 % and so it provides a conservative estimate of the heat transfer coefficient.
In many condensers, tubes are placed above each other. The condensate from one tube drips onto the tube below, which increases the thickness of the film and reduces the heat transfer coefficient. Equation 7.11 has been modified to account for a tube bank that is N tubes high by dividing the term in brackets by the number of tubes in the vertical direction:
(7.14)
Condenser fins are often added to increase the area and the overall heat transfer coefficient. A schematic of a typical finned horizontal tube is shown in Figure 7.6. Cold water flows inside the tubes and refrigerant vapor flows horizontally over the tubes. Refrigerant condensate forms on both the fins and the bare tubing and flows downward.
Figure 7.6 Condensation on finned tubes
For the finned tube geometry, the heat transfer coefficient is given by a relation similar to equation 7.5. An equivalent diameter is employed that accounts for the added heights of the fins. The following relation is recommended (ASHRAE, 2005).
(7.15)
where the characteristic dimension in equation 7.15 is an equivalent fin diameter defined as:
(7.16)
and the effective area is a function of the fin area, prime area, and the fin efficiency. The effective area is
(7.17)
and the effective fin length is the ratio of the area on one side of the fin to the tube diameter.
(7.18)
This rather complicated set of relations for the equivalent diameter of finned tubes has been determined experimentally. In general, the heat transfer coefficients for condensation on finned tubes are somewhat higher than those for bare tubes because the fins are vertical surfaces and the liquid drains better than around a circular tube. However, the main effect of fins is the addition of more surface area. Equations 7.11, 7.14, and 7.15 are general relations that apply to situations in which the condensate drains from the tubes. If the fin spacing is too small, surface tension may cause the liquid to collect and the fluid will not drain and the heat transfer rate will be reduced.
Air and other non-condensables can adversely affect the heat transfer coefficients. Heat transfer coefficients for condensation are generally much higher than for single-phase convective heat transfer, and this usually makes accurate determination of the coefficients less critical. Example 7.4 illustrates the calculation of the condensation heat transfer coefficient for bare and for finned tubes.
"Example 7.5 Determine the heat transfer coefficients and thermal resistances for R-22 condensing on horizontal one-inch diameter tubes for the case of plain and finned tubes. The fins are of copper with a diameter of 1.35 inches, a thickness of 0.004 inches, and a pitch of 10 fins/inch. The saturation temperature of the refrigerant is 85 F and the surface is 80 F."
“Problem specifications”
T_s = 80 “F” “Surface temperature”
T_sat = 85 “F” “Saturation temp.”
DT = T_sat - T_s “F” “Temp. difference”
“Determine the properties of refrigerant for the liquid and vapor phases.”
p_sat = Pressure(R22,x=0, T=T_sat) “psia” “Saturation pressure”
rho_f = 1/Volume(R22,x=0, T=T_sat) “lbm/ft3” “Density”
rho_g = 1/Volume(R22,x=1, T=T_sat) “lbm/ft3” “Density”
cp_f = specheat(R22,T=T_sat, x = 0) “Btu/lbm-F” “Specific heat”
k_f = Conductivity(R22,x=0, P=P_sat) “Btu/hr-ft-F” “Thermal conductivity”
mu_f = Viscosity(R22, x=0, P=P_sat) “lbm/hr-ft” “Viscosity”
h_f = Enthalpy(R22,x=0, T=T_sat) “Btu/lbm” “Enthalpy”
h_g = Enthalpy(R22, x=1, T=T_sat) “Btu/lbm” “Enthalpy”
h_fg = h_g - h_f “Btu/lbm” “Latent heat of vapor.”
“Determine the effective latent heat of vaporization from equation 7.12”
h_fg_prime = h_fg+ 0.68*cp_f*DT “Btu/lbm” “Effective latent heat”
“To determine the unit resistances use one foot as the length of the tube.”
L = 1 “ft” “Length”
D = 1*convert(in,ft) “ft” “Diameter”
“Convert gravitational attraction from a per second to a per hour basis”
g = 32.2*convert(ft/s^2, ft/hr^2) “ft/hr2” “Gravity”
"Determine the thermal resistance of the bare tube. The Nusselt number is calculated using equation 7.14"
N_u_bare = 0.728*(g*rho_f*(rho_f - rho_g)*d^3*h_fg_prime/(k_f*mu_f*DT))^0.25“Nusselt number”
N_u_bare =h_tube*D/k_f “Nusselt number”
A_tube = pi*D*L “ft2” “Area”
R_tube = 1/(h_tube*A_tube) “hr-F/Btu” “Thermal resistance”
“Results
The modified heat of vaporization accounts for cooling the vapor from 82 F to 80 F, and is 77.2 Btu/lbm. The Nusselt number for the bare tubes is 743 and the heat transfer coefficient is 420 Btu/hr-ft2-F. The area of the tube per foot of length is 0.26 ft2, yielding a resistance per foot of length of 0.00910 hr-F/Btu.”
"Determine the thermal resistance of finned tubes. The Nusselt number is determined using equation 7.15"
N_u_fin = 0.689*(rho_f^2*g*D_eq^3*h_fg_prime/(k_f*mu_f*DT))^0.25 “Nusselt number”
N_u_fin = h_fin*D_eq/k_f “Nusselt number”
“The effective diameter and area is found using equations 7.16, 7.17, and 7.18”
1/D_eq^0.25 = 1.3*A_allfins*eta_fin/(A_eff*L_mf^0.25) + A_p/(A_eff*D^0.25) “Equivalent D”
A_eff = A_allfins*eta_fin + A_p “ft2” “Area”
“The fin parameters are needed in order to find fin efficiency from Figure 13.8 The thermal conductivity of the fins is that for copper. The equations are not coupled and can be solved sequentially.”
k_fin = 230 “Btu/hr-ft-F” “Thermal conductivity”
Parameter_fin = m_fin*(r_2c - r_1) “Fin parameter”
m_fin = sqrt(2*h_fin/(k_fin*t_fin)) “1/ft” “Fin parameter”
r_2c = D_fin/2 “ft” “Radius”
r_1 = D/2 “ft” “Radius”
D_ratio = r_2c/r_1 “Diameter ratio”
“From Figure 7.8, the fin efficiency for this diameter ratio and fin parameter is found”
eta_fin = 0.67 “Fin efficiency”
“Determine the effective length and area of the fins. The pitch is 10 fins/inch.“
L_mf =(A_fin/2)/D”ft” “Effective length”
D_fin = 1.35*convert(in,ft) “ft” “Fin diameter”
A_p = pi*D*(L - 10*12*t_fin) “ft2” “Area”
t_fin = 0.01*convert(in,ft) “ft” “Fin thickness”
A_fin = 2* pi*((D_fin+t_fin)^2 - D^2)/4 “ft2” “Area”
A_allfins = A_fin*FPI*L “ft2” “Area”
FPI = 10*convert(1/in,1/ft) “1/ft” “Pitch”
R_fin = 1/(h_fin*A_eff) “hr-F/Btu” “Thermal resistance”
eta_overall = 1 - (A_allfins/(A_allfins + A_p))*(1 - eta_fin) “Overall efficiency”
R_finnedtube = 1/(h_fin*eta_overall*(A_allfins + A_p)) “hr-F/Btu” “Thermal resistance”
Results and Discussion:
The total fin area per foot of tube length is 1.112 ft2. The area not covered by the fins, which is the tube surface area less that covered by the base of 120 fins, is 0.236 ft2 per foot of length. The effective area per foot of length is 0.981 ft2, the effective fin length is 0.0556 ft, and the equivalent diameter is 0.0264 ft. The Nusselt number for the finned tubes is 300, yielding a condensing heat transfer coefficient of 535 Btu/hr-ft2-F. The fin and overall efficiencies are determined to be 0.670 and 0.727 respectively. The thermal resistance per foot of length for the finned tubes is 0.00190 hr-F/Btu.
Condensation inside horizontal tube is more complicated than that for condensation outside the tubes. The formation of the condensate is affected by the flow of fluid through the tube. A different set of flow regimes exist depending on the flow rate of the fluid through the tube. Typical two-phase flow patterns for flow in horizontal tubes for low and high mass velocity (flow rate per unit area) are shown in Figure 7.7.
Figure 7.7 Flow regimes for condensation in horizontal tubes
When the mass velocity of the flow is low, there is initially a region where the superheated vapor is cooled to the dew point. Condensation then forms around the periphery of the tube and, due to the shear at the liquid and vapor interface, flows axially down the tube. The liquid at the top of the tube also drains downward due to gravity, creating an annular flow pattern, and the cross-sectional pattern is as shown in Figure 7.8. The angle q represents the fraction of the tube wall on which condensation occurs. All vapor eventually condenses and the liquid flows axially out of the tubes. When the mass flux is high, the superheated section is relatively longer. The liquid condensate fills the tube with bubbles of vapor entrained in the liquid that eventually condense. The liquid becomes subcooled and flows from the tube.
Figure 7.8 Annular flow pattern for condensation in horizontal tube
The heat transfer during condensation involves two types of mechanisms. One is film condensation similar to that which occurs on the outside of a horizontal cylinder, discussed above. The other mechanism is convective condensation, which is due to the axial flow of condensate along the channel and is similar to that for forced convection in tubes, discussed in Section 4.3. The heat transfer coefficients for film and axial flow condensation are applied to their respective areas. Flow pattern maps have been developed by Hajal, et al. (2003) and Thome et al. (2003) that show the transition boundaries for different flow regimes such as wavy, stratified, and mist. Only a brief summary of the basic ideas will be given in this text.
For the upper portion of the tube where film condensation occurs, the film is very thin and the heat transfer coefficients are high. The thickness of the falling film is given by
(7.19)
where D is the tube diameter and e is the void fraction (the vapor fraction of the mixture by volume). The void fraction is directly related to the quality x and the densities of the two phases.
(7.20)
The falling film condensation coefficient is given by equation 7.11, repeated here
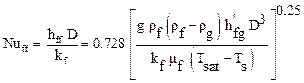(7.21)
The convection flow heat transfer coefficient is given by a relation similar to that for forced convection in tubes
(7.22)
where dL is the thickness of the liquid at the bottom of the tube and fi is an interfacial roughness factor that accounts for the shear between the vapor and liquid. The Reynolds number is determined using the thickness of the liquid layer as the characteristic dimension
(7.23)
where G is the mass flux. The Prandtl number is defined using the properties of the liquid:
(7.24)
The interfacial roughness factor fi is about unity for thin films and increases as the ratio of the vapor velocity to liquid velocity increases. It has been correlated as
(7.25)
where s is the surface tension and accounts for the damping effect of surface tension on surface waves created by the movement of vapor over the liquid.
For stratified flow, such as shown in Figure 7.8, the thickness of the layer depends on the relative amounts of vapor and liquid. A correlation for the angle q of the condensing vapor fraction as a function of the quality has been obtained, and is shown in Figure 7.9. Even at a low value of quality the angle of the condensing layer is greater than 180 degrees and the fraction of the tube exposed to the condensing layer is over 50 %.
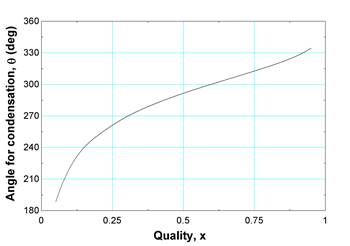
Figure 7.9 Angle of condensing layer for stratified flow
The thickness of the liquid layer is related to the angle of the condensing vapor fraction through the geometry shown in Figure 7.8. The geometric relation for height of the liquid layer as a function of the angle for the film condensation portion is
(7.26)
The expression for the thickness of the liquid layer allows the convective heat transfer coefficient to be determined. The overall heat transfer coefficient is then a sum of the condensing and convective heat transfer coefficients weight by the respective heat transfer areas.
The basic ideas behind the mechanisms of condensation in tubes have been presented in this section. Although the heat transfer coefficients can be estimated using these relations, it is recommended that the original references (Hajal, et al., 2003; Thome et al., 2003) be consulted. These references describe flow pattern maps that describe the different flow regimes in a tube at different axial positions and lead to a more accurate evaluation of the local heat transfer coefficient as a function of axial position. The condensation phenomenon is obviously very complicated and the calculation process yields local values at an axial position that must then be integrated over the length of the tube. The modern design of condensers is based on these ideas. Example 7.6 illustrates the calculation procedure when a number of the parameters are known.
"Example 7.6 Estimate the heat transfer coefficients for R-134a condensing inside the tubes of an air-cooled condenser at a position where the quality is 60 %. The flow rate per tube is 0.0025 kg/s, the tube diameter is 8 mm, the saturation temperature is 40 C, the surface temperature is 35 C, and the interface roughness factor is 1.2. "
"Problem specifications"
T_s = 38 “C” “Temperature”
T_sat = 40 “C” “Temperature”
DT = T_sat - T_s “C” “Temp. difference”
p_sat = Pressure(R134a,x=0, T=T_sat) “kPa” “Pressure”
x = 0.6 “Quality”
D = 8*convert(mm,m) “m” “Tube diameter”
m_dot = 0.0025 “kg/s” “Mass flow rate”
f_i = 1.2 “Interfacial roughness”
g = 9.8 “m/s2” “Gravity”
"Determine the refrigerant properties for both the liquid and vapor phases"
rho_f = density(R134a,x=0, T=T_sat) “kg/m3” “Density”
rho_g = density(R134a,x=1, T=T_sat) “kg/m3” “Density”
h_f = Enthalpy(R134a,x=0, T=T_sat) “kJ/kg” “Enthalpy”
h_g = Enthalpy(R134a, x=1, T=T_sat) “kJ/kg” “Enthalpy”
h_fg = h_g - h_f “kJ/kg” “Latent heat”
cp_f = specheat(R134a,T=T_sat, x = 0) “kJ/kg-C” “Specific heat”
k_f = Conductivity(R134a,T=T_sat, x=0) “W/m_C” “Thermal conductivity”
mu_f = Viscosity(R134a, T=T_sat , x=0) “kg/m-s” “Viscosity”
“Determine the effective latent heat of vaporization from equation 7.12”
h_fg_prime = h_fg+ 0.68*cp_f*DT “kJ/kg” “Effective latent heat”
"The void fraction is given by equation 7.20"
Void = 1/(1+((1-x)/x)*(rho_g/rho_f)) “Void fraction”
"The heat transfer coefficient is needed for both the falling film condensation and the convective flow along the bottom of the tube. The condensation coefficient is computed first. The Nusselt number for the film condensation portion is given by equation 7.21. The equations are not coupled and can be solved sequentially."
N_u_film = 0.728*(g*rho_f*(rho_f - rho_g)*d^3*h_fg*convert(kJ,J)/(k_f*mu_f*DT))^0.25 “Nusselt”
N_u_film =h_film*D/k_f “Nusselt number”
"The thickness of the falling film is given by equation 7.19"
delta_ff = D*(1-void)/4 “m” “Falling film thickness”
"The convective condensation coefficient and angle of contact of the condensate layer are determined next. The angle of the condensate layer is taken from Figure 7.9."
Theta = 300* convert(deg,rad) “rad” “Layer angle”
delta_L = D*0.5*(1-cos((2*Pi-theta)/2)) “m” “Layer thickness”
D_ratio = delta_L/D “Relative thickness”
“The Reynolds number is given by equation 7.23, with the mass flux determined from the mass flow rate and cross-sectional area. The Nusselt number is then given by equation 7.22 and the convection coefficient is computed using the Nusselt number and the thickness of the layer. "
G_flow = m_dot/A “kg/m2-s” “Mass flux”
A = Pi*D^2/4 “m2” “Cross-sectional area”
Re = 4*G_flow*(1-x)*delta_L/((1-void)*mu_f) “Reynolds number”
Pr = cp_f*convert(kJ,J)*mu_f/k_f “Prandtl number”
N_u_conv = C*Re^n*Pr^m*f_i “Nusselt number”
C=0.003 “Coefficient”
n = 0.74 “Exponent”
m = 0.5 “Exponent”
N_u_conv = h_conv*delta_L/k_f “Nusselt number”
"The overall condensation coefficient is the sum of the falling film and convective coefficients weighted by the area of the tube (represented by the angle) for each mechanism"
h_overall=h_film*(Theta/(2*Pi))+h_conv*(2*Pi-Theta)/(2*Pi) “W/m2-C” “Overall coefficient”
Results and Discussion
For the falling film section of the tube, the Nusselt number is 330 and the heat transfer coefficient is 3122 W/m2-C. The thickness of the falling film depends on the void fraction, which is 0.972, which means that the volume of the refrigerant vapor is 97 % of the tube volume at this location. The film thickness is 0.000057 m. The falling film is very thin and the thickness is about 0.6% of the tube diameter.
The Reynolds number for the convective flow is a function of the thickness of the liquid layer which in turn depends on the angle of the condensation layer as shown in Figures 7.8 and 7.9. For a quality of 0.6 the angle is 300 degrees or 5.24 radians. The liquid layer thickness is 0.000546 m, which is about 7 % the thickness of the tube diameter. The mass flux is 49.7 kg/m2-s and the Reynolds number is 9350. The Nusselt number is 5.58 and the convective heat transfer coefficient for the layer at the bottom of the tube is 788 W/m2-C.
SM 7.7 Pressure Drops in Two-Phase Flows
The pressure drop due to a single phase flow of a fluid through a pipe is due to wall friction and to fittings, and relations for determining the pressure drop are presented in Chapter 3. In two-phase flow there are additional mechanisms that come into play and that need to be accounted for in the pressure drop evaluation. The wall friction relations are different since both liquid and vapor flow through the pipe and the flow patterns are different from those of single phase flows. For example, in annular condensation flow there is a thin layer of liquid between the wall and the vapor that affects the wall friction. The second mechanism is the change in momentum of the flow due to evaporation or condensation, even if the cross-sectional area of the pipe is constant. For example, in the tubes of an evaporator the entering fluid is mostly liquid phase and has a relatively low velocity and, consequently, momentum. As the liquid evaporates into vapor the density decreases significantly and the velocity increases. The corresponding momentum increase is a result of the pressure forces on the fluid, and so the momentum of the vapor leaving the tube is relatively high and the pressure is low. Similarly, for condensation, the momentum of the flow decreases in the flow direction and the pressure rises.
One approach to estimating the pressure drops in two-phase flows is to modify the relationships for single phase flows. In some of the approaches a multiplier for the single phase pressure drop is employed. Other relationships are based on a set of empirical relations that add to the single phase relation. For all of the correlations, the differences between the calculated and measured pressure drops can be as high as 50 %. The Muller-Steinhagen and Heck correlation (ASHRAE, 2005) has been found to work quite well with a database consisting of flows of refrigerants and steam as well as mixtures of air, water, and/or oil in horizontal tubes, and is presented here.
The correlations are presented as the pressure gradient rather than the pressure difference over the flow length. The properties of the flow such as quality and void fraction change as the fluid flows through a pipe and so the local value of the pressure gradient needs to be integrated to obtain the total pressure drop. The Muller-Steinhagen and Heck correlation is give as
(7.27)
where p is the pressure, z is the coordinate along the flow length, x is the quality, and the subscript lo denotes the liquid phase only. The term L is a combination of the liquid and vapor phase pressure gradients and given as
(7.28)
The liquid and vapor only pressure gradients are determined using the conventional relations with friction factor, mass flux, and fluid properties (Chapter 3).
(7.29)
and
(7.30)
where flo and fvo are the friction factors for liquid only and vapor only flows, respectively, at the total mass flux GT and rl and rv are the liquid and vapor densities at the local pressure and temperature, respectively. The friction factors are computed using the relation (Chapter 3) of
(7.31)
where the Reynolds number is defined using the total mass flux and the liquid or vapor viscosity, as appropriate.
(7.32)
The estimation of the pressure gradient is given in Example 7.7 for the condensation conditions described in Example 7.6.
"Example 7.7 Estimate the pressure gradient for R-134a condensing inside the tubes of an air-cooled condenser at a position where the quality is 60 %. The flow rate per tube is 0.0025 kg/s, the tube diameter is 8 mm, the saturation temperature is 40 C, and the surface temperature is 35 C.
The equations are not coupled and can be solved sequentially. "
“Problem specifications”
T_sat = 40 “C” “Temperature”
x = 0.6 “Quality”
D = 8*convert(mm,m) “m” “Tube diameter”
m_dot = 0.0025 “kg/s” “Mass flow rate”
“Determine the refrigerant properties for both the liquid and vapor phases.”
rho_f = density(R134a,x=0, T=T_sat) “kg/m3” “Density”
rho_g = density(R134a,x=1, T=T_sat) “kg/m3” “Density”
mu_f = Viscosity(R134a, T=T_sat , x=0) “kg/m-s” “Viscosity”
mu_g = Viscosity(R134a, T=T_sat , x=1) “kg/m-s” “Viscosity”
“Determine the mass flux based on the mass flow rate and cross-sectional area”
G_tot = m_dot/A_c “kg/m2-s” “Mass flux”
A_c = pi*D^2/4 “m2” “Cross-sectional area”
"The liquid phase pressure gradient is from equation 7.29 with the friction factor from equation 7.31. The Reynolds number is based on the total mass flux and the liquid viscosity."
Re_l = G_tot*D/mu_f “Reynolds number”
f_l = 0.079*Re_l^(-0.25) “Friction factor”
dpdz_l = -f_l*2*G_tot^2/(d*rho_f) “Pa/m” “Pressure gradient”
"The vapor phase pressure gradient is from equation 7.30 with the friction factor from equation 7.31. The Reynolds number is based on the total mass flux and the vapor viscosity."
Re_v = G_tot*D/mu_g “Reynolds number”
f_v = 0.079*Re_v^(-0.25) “Friction factor”
dpdz_v =- f_v*2*G_tot^2/(d*rho_g) “Pa/m” “Pressure gradient”
"The total pressure gradient is form equation 7.27 with Lambda calculated from equation 7.28"
Lambda = dpdz_l + 2* (dpdz_v - dpdz_l)*x
dpdz = lambda*(1-x)^(1/3)+dpdz_l*x^3 “Pa/m” “Pressure gradient”
Results and Discussion
The fluid properties and mass flux are the same as in Problem 7.6. For the liquid only pressure gradient, the Reynolds number is 2469 and the friction factor is 0.0112. The corresponding pressure gradient is – 6.04 Pa/m. The Reynolds number for the vapor only calculation is 31,320, the friction factor 0.00594, and the pressure gradient -73.3 Pa/m.
The pressure gradient depends on the parameter L which is – 86.8 Pa/m. The pressure gradient at the location where the quality is 0.6 is then – 65.2 Pa/m.
Example 7.7 shows how the local pressure gradient is estimated. To determine the overall pressure drop, the pressure gradient needs to be integrated over the tube length. This involves evaluating the quality along the tube length. Determining the quality as a function of length requires an energy balance on the flow. The quality at a position depends on the total heat transfer to or from the flow which depends on the heat transfer coefficient. Although the process is involved, the heat transfer and pressure gradient relations presented here will allow the total pressure drop to be estimated.
SM 7.8 Summary
Condensers and evaporators are sensible heat exchangers in which the refrigerant changes phase. The capacitance rate during a phase change is effectively infinite since the fluid energy changes without a corresponding change in temperature. However, the refrigerant is often superheated or subcooled, and the overall capacitance rate ratio is not zero. For evaporators, treating the exchanger as one with a capacity rate ratio of zero is usually sufficiently accurate. In a condenser, there is usually significant desuperheating of the vapor prior to condensation. Dividing the exchanger into two sections, one with a finite capacitance ratio and the other zero, improves the estimation of performance.
In the evaporation and condensation of refrigerants additional mechanisms over those in single phase heat transfer are present. The process of changing phase from liquid to vapor in evaporators and vapor to liquid in condensers affects the flow patterns and, consequently, the heat transfer and pressure drop for the flow. In evaporation on the outside of tubes the phase change takes place at the surface and the rising bubbles create secondary flow patterns in the fluid. For evaporation inside tubes, bubbles forming at the wall surface move to the center of the flow, also causing mixing and secondary current. Condensation on the outside of tubes creates a downward flow of condensate over the surfaces that promotes mixing. For condensation inside tubes there is a layer of condensing liquid along the wall surface and a flow of vapor down the center of the tube, creating a complex flow pattern. The heat transfer coefficient and pressure drop correlations for evaporation and condensation are empirical and bring in the important parameters. They can be used as guides to estimate the heat transfer and pressure drop for these heat transfer situations.
SM 7.9 Nomenclature
A area
Bo* modified boiling number
cp specific heat
cs equivalent specific heat
C capacitance rate, coefficient
C* capacitance rate ratio
Cs surface coefficient
D diameter
f friction factor
fi interfacial roughness factor
F fraction of heat exchanger surface
FFL fluid surface parameter
FPF reduced pressure function
g gravitational attraction
G mass flux
GT total mass flux
hc convection heat transfer coefficient
hfg latent heat of vaporization
hfg’ modified latent heat of vaporization
hSP single phase heat transfer coefficient
hTP two phase heat transfer coefficient
k thermal conductivity
Leff effective fin length
mass flow rate
n exponent
N number of tubes
Ntu number of transfer units for heat transfer
Ntu* number of transfer units for mass transfer
p pressure
Pr Prandtl number
heat flow rate
heat flux (heat flow rate per unit area)
Reynolds number based on hydraulic diameter
Rp roughness
T temperature
U overall unit thermal conductance
U* overall unit mass transfer conductance
V velocity
x quality
z coordinate in flow direction, location where refrigerant is saturated
d film thickness
dL thickness of the liquid layer
Dp pressure drop
e effectiveness, void fraction
hf fin efficiency
overall surface mass transfer efficiency
L pressure drop parameter
q angle
mf fluid viscosity
r density
r* ratio of liquid to vapor density
s surface tension
Subscripts
a air side
D diameter
DH hydraulic diameter
eff effective
eq equivalent
f liquid phase, fin
ff falling film
g vapor phase
i inside, inlet
lo liquid only
o outside, outlet, reference value
r refrigerant, refrigerant side
s surface
sat saturated conditions
vo vapor only
SM 7.10 References
El Hajal, J,, J. R. Thome, and A. Cavallini, “Condensation in Horizontal Tubes, part 1: Two-Phase Flow Pattern Map,” International Journal of Heat and Mass Transfer, Vol 46, p3349-3363, 2003.
Rohsenow, W. M., J. P. Hartnett, and E. N. Ganic', Editors "Handbook of Heat Transfer Fundamentals", Chapters 11 and 12, McGraw Hill, 1985
Thome, J. R., J. El Hajal, and A. Cavallini, “Condensation in Horizontal Tubes, part 2: New Heat Transfer Model based on Flow Regimes,” International Journal of Heat and Mass Transfer, Vol 46, p3365-3387, 2003.
SM 7.11 Problems
Problems in English Units
7.1 An evaporator is used to chill a liquid water flow rate of 200 gpm that enters at 55 F and leaves at 45 F. The refrigerant is R-22 that enters at a quality of 0.1 and a temperature of 30 F and leaves with 5 F superheat. Determine heat transfer rate, the required overall conductance, and the refrigerant mass flow rate. Draw some conclusions from your results.
7.2 Determine the heat flux and heat transfer coefficient for evaporation from the outside of tubes in a flooded R-22 evaporator over a range of saturation temperatures between 10 and 50 F using equation 7.8. The surface temperature is always 10 F higher than the saturation temperature. The surface coefficient Cs is 0.02. Draw some conclusions from your results.
7.3 A flooded R-22 evaporator is designed with tubes that are 10 feet long, have an OD of 0.75 inch and an ID of 0.65 inch.. The water flow rate is 1 gpm per tube and the water enters at 60 F. The refrigerant temperature is 30 F. Determine the heat transfer coefficient for the water side of the evaporator, the heat transfer coefficient for the refrigerant side of the evaporator, the exchanger effectiveness, and the water outlet temperature. Determine how many tubes are needed for a cooling capacity of 10 tons. Draw some conclusions from your results.
7.4 Determine the heat transfer coefficient, heat flux, and pressure gradient inside the 0.5-inch diameter tubes of a DX coil at a location where the quality is 0.4. The refrigerant is R-134a, the saturation pressure is 45 psia, the wall temperature is 50 F, the tubes are aluminum, and the mass flow rate through each tube is 200 lb/hr. Draw some conclusions from your results.
7.5 Determine the heat transfer coefficient, heat flux, and pressure gradient inside the 0.5-inch diameter copper tubes of a DX coil as a function of quality over the range of 0 to 0.8. The refrigerant is R-134a, the saturation pressure is 45 psia, the wall temperature is 50 F and the mass flow rate through each tube is 200 lb/hr. Draw some conclusions from your results.
7.6 Estimate the boiling heat flux and heat transfer coefficient inside the 0.5-inch diameter copper tubes of a DX coil from the entrance (saturated liquid) to the exit (saturated vapor) at a mass flow rate of 100 lb/hr.. The refrigerant is R-113, the saturation temperature is 35 F, and the wall temperature is 45 F. Estimate the length of tube needed to achieve the complete phase change and the velocities at the entrance and exit of the tube. Plot the quality and heat transfer coefficient as functions of distance along the tube. Draw some conclusions from your results.
7.7 A water-cooled R-134a condenser is designed to transfer 200,000 Btu/hr of heat at a condensing temperature of 105 F. The water flow is designed for an entering temperature of 90 F and a temperature rise of 10 F. The surface has an overall conductance of 500 Btu/hr-ft2-F. Determine the refrigerant condensing temperature, the water flow rate and the heat transfer area for the condenser. Draw some conclusions from your results.
7.8 A water cooled R-22 condenser is made of 60 unfinned horizontal copper tubes that are 10 feet long. The heat transfer rate is 120,000 Btu/hr. The tube OD is 0.75 inch and the ID is 0.65 inch. The water flow rate is 0.5 gpm per tube and the water enters at 85 F. Determine the refrigerant saturation temperature, heat transfer coefficient for the water side of the condenser, heat transfer coefficient for the refrigerant side of the condenser, the condenser effectiveness, the water outlet temperature, and the refrigerant flow rate. Draw some conclusions from your results.
7.9 Design a water cooled R-22 condenser with a heat rejection rate of 50,000 Btu/hr made of unfinned horizontal copper tubes that have an OD of 0.75 inch and an ID of 0.65 inch. The refrigerant saturation temperature is 95 F and the inlet water temperature is 80 F. Select a water flow rate, tube length, and number of tubes that will meet the design specifications. The water flow rate should be between 0.1 and 2 gpm per tube and the tube length should be between 4 and 10 feet. Draw some conclusions from your results.
7.10 For a R-134a condenser made of bare horizontal tubes determine and plot the heat transfer coefficient duct and the hA product per unit length over the range of saturation temperatures from 70 to 120 F C for tubes that range in diameter between 0.5 inch and 2 inch in diameter. The surface temperature is always 5 F lower than the saturation temperature. Draw some conclusions from your results.
7.11 Determine the heat transfer coefficient and heat transfer per unit length for R-134a condensing on horizontal 0.75 in. diameter tubes for bare and finned tubes. The fins are made of aluminum, are 1.5 in. in diameter and 0.050 in. thick, and have a pitch of 10 fpi. The saturation temperature of the refrigerant is 95 F and the surface is 90 F. Draw some conclusions from your results.
7.12 Estimate the heat transfer coefficient and pressure gradient for R-134a condensing inside the tubes of an air-cooled condenser at a position where the quality is 0.5. The flow rate is 20 lbm/hr, the tube diameter is 0.4 inch, the saturation temperature is 100 F, the surface temperature is 90 F and the interface roughness factor is 1.2. Draw some conclusions from your results.
7.13 Estimate the heat transfer coefficient and pressure gradient for R-134a condensing inside the tubes of an air-cooled condenser at a position over the range of quality of 1.0 to 0. The flow rate is 20 lbm/hr, the tube diameter is 0.4 inch, the saturation temperature is 100 F, the surface temperature is 90 F and the interface roughness factor is 1.2. Draw some conclusions from your results.
7.14 Estimate the tube length required to condense R-134a entering as a vapor and leaving as liquid. The flow rate is 20 lbm/hr, the tube diameter is 0.4 inch, the saturation temperature is 100 F, the surface temperature is 90 F and the interface roughness factor is 1.2. Draw some conclusions from your results.
Problems in SI units
7.15 An evaporator is used to chill a liquid water flow rate of 10 kg/s that enters at 13 C and leaves at 8 C. The refrigerant is R-22 that enters at a quality of 0.1 and a temperature of 4 C and leaves with 3 C superheat. Determine heat transfer rate, the required overall conductance, and the refrigerant flow rate. Draw some conclusions from your results.
7.16 Determine the heat flux and heat transfer coefficient for evaporation from the outside of tubes in a flooded R-22 evaporator over a range of saturation temperatures between 0 and 30 C using equation 7.8. The surface temperature is always 5 C higher than the saturation temperature. The surface coefficient Cs is 0.02. Draw some conclusions from your results.
7.17 A flooded R-22 evaporator is designed with tubes that are 2 m long, have an OD of 20 mm and an ID of 17 mm. The water flow rate is 0.05 kg/s per tube and the water enters at 20 C. The refrigerant temperature is 5 C. Determine the heat transfer coefficient for the water side of the evaporator, the heat transfer coefficient for the refrigerant side of the evaporator, the exchanger effectiveness, and the water outlet temperature. Determine how many tubes are needed for a cooling capacity of 30 kW. Draw some conclusions from your results.
7.18 Determine the heat transfer coefficient and pressure gradient inside the 1 cm diameter copper tubes of a DX coil at a location where the quality is 0.4. The refrigerant is R-134a, the saturation pressure is 300 kPa, the wall temperature is 10 C, and the mass flow rate through each tube is 0.03 kg/s. Draw some conclusions from your results.
7.19 Determine the heat flux, heat transfer coefficient and pressure gradient inside the 1 cm diameter copper tubes of a DX coil as a function of location over the range of quality between 0 and 0.8. The refrigerant is R-134a, the saturation pressure is 300 kPa, the wall temperature is 10 C, and the mass flow rate through each tube is 0.03 kg/s. Draw some conclusions from your results.
7.20 Estimate the boiling heat flux and heat transfer coefficient inside the 1 cm diameter copper tubes of a DX coil from the entrance (saturated liquid) to the exit (saturated vapor) at a mass flow rate of 0.1 kg/s.. The refrigerant is R-113, the saturation temperature is 5 C, and the wall temperature is 8 C. Estimate the length of tube needed to achieve the complete phase change and the velocities at the entrance and exit of the tube. Plot the quality and heat transfer coefficient as functions of distance along the tube. Draw some conclusions from your results.
7.21 A water-cooled R-22 condenser is designed to transfer 50 kW of heat at a condensing temperature of 45 C. The water flow is designed for an entering temperature of 30 C and a temperature rise of 5 C. The surface has an overall conductance of 2500 W/m2-C. Determine the refrigerant condensing temperature, the water flow rate and the heat transfer area for the condenser. Draw some conclusions from your results.
7.22 A water cooled R-22 condenser is made of 60 unfinned horizontal copper tubes that are 3 m long. The heat transfer rate is 40 kW. The tube OD is 22 mm and the ID is 20 mm. The water flow rate is 0.05 kg/s per tube and the water enters at 30 C. Determine the refrigerant saturation temperature, heat transfer coefficient for the water side of the condenser, heat transfer coefficient for the refrigerant side of the condenser, the condenser effectiveness, the water outlet temperature, and the refrigerant flow rate. Draw some conclusions from your results.
7.23 Design a water cooled R-22 condenser with a heat rejection rate of 20 kW made of unfinned horizontal copper tubes that have an OD of 22 mm and an ID of 20 mm. The refrigerant saturation temperature is 35 C and the inlet water temperature is 20 C. Select a water flow rate, tube length, and number of tubes that will meet the design specifications. The water flow rate should be between 0.5 and 5 kg/s per tube and the tube length should be between 1 and 3 m. Draw some conclusions from your results.
7.24 For a R-134a condenser made of bare horizontal tubes determine and plot the heat transfer coefficient duct and the hA product per unit length over the range of saturation temperatures from 20 to 60 C for tubes that range in diameter between 10 mm and 5 mm diameter. The surface temperature is always 3 C lower than the saturation temperature.
7.25 Determine the heat transfer coefficient and heat transfer per unit length for R-134a condensing on horizontal 20 mm diameter tubes for bare and finned tubes. The fins are made of aluminum, are 40 mm in diameter, 1.5 mm. thick, and have a pitch of 25 fins/cm. The saturation temperature of the refrigerant is 35 C and the surface is 32 C. Draw some conclusions from your results.
7.26 Estimate the heat transfer coefficient and pressure gradient for R-134a condensing inside the tubes of an air-cooled condenser at a position where the quality is 0.5. The flow rate is 0.0025 kg/s, the tube diameter is 8 mm, the saturation temperature is 40 C, the surface temperature is 35 C, and the interface roughness factor is 1.2. Draw some conclusions from your results.
7.27 Estimate the heat transfer coefficient and pressure gradient for R-134a condensing inside the tubes of an air-cooled condenser at a position over the range of quality of 1.0 to 0. The flow rate tube is 0.0025 kg/s, the tube diameter is 8 mm, the saturation temperature is 40 C, the surface temperature is 35 C and the interface roughness factor is 1.2. Draw some conclusions from your results.
7.28 Estimate the tube length required to condense R-134a entering as a vapor and leaving as liquid. The tube diameter is 8 mm, the flow rate is 0.0025 kg/s, the saturation temperature is 40 C, the surface temperature is 35 C and the interface roughness factor is 1.2. Draw some conclusions from your results.
Source: http://higheredbcs.wiley.com/legacy/college/mitchell/0470624574/online_chap/ch07.doc
Web site to visit:http://higheredbcs.wiley.com
Author of the text: indicated on the source document of the above text
If you are the author of the text above and you not agree to share your knowledge for teaching, research, scholarship (for fair use as indicated in the United States copyrigh low) please send us an e-mail and we will remove your text quickly. Fair use is a limitation and exception to the exclusive right granted by copyright law to the author of a creative work. In United States copyright law, fair use is a doctrine that permits limited use of copyrighted material without acquiring permission from the rights holders. Examples of fair use include commentary, search engines, criticism, news reporting, research, teaching, library archiving and scholarship. It provides for the legal, unlicensed citation or incorporation of copyrighted material in another author's work under a four-factor balancing test. (source: http://en.wikipedia.org/wiki/Fair_use)
The information of medicine and health contained in the site are of a general nature and purpose which is purely informative and for this reason may not replace in any case, the council of a doctor or a qualified entity legally to the profession.
The texts are the property of their respective authors and we thank them for giving us the opportunity to share for free to students, teachers and users of the Web their texts will used only for illustrative educational and scientific purposes only.
All the information in our site are given for nonprofit educational purposes