Gas Turbine System and Propulsion

GAS TURBINE

Axial Turbine

Introduction:-

            A gas turbine unit for power generation or a turbojet engine for production of thrust primarily consists of a compressor, Combustion chamber and a turbine. The air as it passes through the compressor, experiences an increase in presser. There after the air in fed to the combustion chamber leading to tan increase in temperature. This high pressure and temperature gas in then passed through the turbine, where it is expanded the required power is obtained.

Turbines, like compressors, can be classified into radial, axial and mixed flow machines.  In the axial machine the fluid moves essentially in the axial direction through the rotor. In the radial type the fluid motion is mostly radial. The mixed-flow machine is characterized by a combination of axial and radial motion of the fluid relative to the rotor. The choice of turbine type depends on the application, though it is not always clear that any one type is superior.
Comparing axial and radial turbines of the same overall diameter, we may say that the axial machine, just as in the case of compressors, is capable of handling considerably greater mass flow. On the other hand, for small mass flows the radial machine can be made more efficient than the axial one. The radial turbine is capable of a higher pressure ratio per stage than the axial one. However, multistaging is very much easier to arrange with the axial turbine, so that large overall pressure ratios are not difficult to obtain with axial turbines. In this chapter,

We will focus on the axial flow terbine

Generally the efficiency of a well-designed turbine is higher than the efficiency of a compressor. Moreover, the design process is somewhat simpler. The principal reason
For this fact is that the fluid undergoes a pressure drop in the turbine and a pressure rise in the compressor .The pressure drop in the turbine is sufficient to keep the secondary layer generally well behaved and the secondary layer separation which of the occurs in compressors because of an adverse pressure gradient, can be avoided in turbines. Offsetting this advantage is the much more critical stress problem, since turbine rotors must operate in very high temperature gas. Actual blade shape is often more dependent on stress and cooling considerations than on aerodynamic considerations, beyond the satisfaction of the velocity-triangle requirements.
Because of the generally falling pressure in turbine flow passages much more turbine in a giving blade row is possible without danger of flow separation than in an axial compressor blade row. This means much more work and considerably higher pressure ratio, per stage.
In recent years advances have been made in turbine blade cooling and in the metallurgy of turbine blade materials. This means that turbines are able to operate successfully at increasingly high inlet gas temperatures and that substantial improvements are being made in turbine engine thrust, weight, and fuel consumption.

Two-dimensional theory of axial flow turbine.

An axial turbine stage consists of a row of stationary blades, called nozzles or stators, followed by the rotor, as Fig 1 illustrates. Because of the large pressure drop per stage, the nozzle and rotor blades may be of increasing length, as shown, to accommodate the rapidly expanding gases, while holding the axial velocity to something like a uniform value through the stage.

It should be noted that the hub–lip ratio for a high pressure gas turbine in quite high that in it is having blades of short length. Thus, the radial variation in velocity and pressure may be neglected and the performance of a turbine stage is calculated from the performance of the blading at the mean radial section that in a bio-dimensional “pitch-line

 

Source: http://www.nptel.ac.in/courses/112104117/chapter_4/GAS%20TURBINE.doc

Web site to visit: http://www.nptel.ac.in

Author of the text: indicated on the source document of the above text

 

 

Lecture-6
Compressors

 

In Chapter 15, we discussed the basic fluid mechanical principles governing the energy transfer in a fluid machine. A brief description of different types of fluid machines using water as the working fluid was also given in Chapter 15. However, there exist a large number of fluid machines in practice, that use air, steam and gas (the mixture of air and products of burnt fuel) as the working fluids.  The density of the fluids change with a change in pressure as well as in temperature as they pass through the machines. These machines are called ‘compressible flow machines’ and more popularly ‘turbomachines’. Apart from the change in density with pressure, other features of compressible flow, depending upon the regimes, are also observed in course of flow of fluids through turbomachines. Therefore, the basic equation of energy transfer (Euler’s equation, as discussed in Chapter-15) along with the equation of state relating the pressure, density and temperature  of the working fluid and other necessary equations of compressible flow, (as discussed in Chapter-14) are needed to describe the performance of a turbomachine. However, a detailed discussion on all types of turbomachines is beyond the scope of this book. We shall present a very brief description of a few compressible flow machines, namely, compressors, fans and blowers in this chapter.

Centrifugal Compressors
A centrifugal compressor is a radial flow rotodynamic fluid machine that uses mostly air as the working fluid and utilizes the mechanical energy imparted to the machine from outside to increase the total internal energy of the fluid mainly in the form if increased static pressure head.
During the second world war most of the gas turbine units used centrifugal compressors. Attention was focused on the simple turbojet units where low power-plant weight was of great importance. Since the war, however, the axial compressors have been developed to the point where it has an appreciably higher isentropic efficiency. Though centrifugal compressors are not that popular today, there is renewed interest in the centrifugal stage, used in conjunction with one or more axial stages, for small turbofan and turbopop aircraft engines.
A centrifugal compressor essentially consists of three components.

1. A stationary casing
2. A rotating impeller as shown in Fig. 16.1 (a) which imparts a high velocity to the air. The impeller may be single or double sided as show in fig. 16.1 (b) and (c) but the fundamental theory is same for both.
3. A diffuser consisting of a number of fixed diverging passages in which the air is decelerated with a consequent rise in static pressure.

 

Principle of operation: Air is sucked into the impeller eye and whirled outwards at high speed by the impeller disk. At any point in the flow of air through the impeller the centripetal acceleration is obtained by a pressure head so that the static pressure of the air increases from the eye to the tip of the impeller. The remainder of the static pressure rise is obtained in the diffuser, where the very high velocity of air leaving the impeller tip is reduced to almost the velocity with which the air enters the impeller eye.
Usually, about half of the total pressure rise occurs in the impeller and the other half in the diffuser. Owing to the action of the vans in carrying the air around with the impeller, there is a slightly static pressure on the forward side of the vane than on the trailing face. The air will thus tend to flow around the edge of the vanes in the clearing space between the impeller and casing. This result in a loss of efficiency and the clearance must be kept as small as possible. Sometimes, a shroud attached to the blades as shown in Fig. 16.1 (d) may eliminate such a loss, but it is avoided because of increased disc friction loss and of manufacturing difficulties.
The straight and radial blades are usually employed to avoid any undesirable bending stress to be set up in the blades. The choice of radial blades also determines that the total pressure rise is divided equally between impeller and diffuser.

Work done and pressure rise
Since no work is done on the air in the diffuser, the energy absorbed by the compressor will be determined by the conditions of the air at the inlet and outlet of the impeller. At the first instance, it is assumed that the air enters the impeller eye in the axial direction, so that the initial angular momentum of the air is zero. The axial portion of the vanes must be curved so that the air can pass smoothly into the eye. The angle which the leading edge of a vane makes with the tangential direction,a, will be given by the direction of the relative velocity of the air at inlet, , as shown in Fig. 16.2. The air leaves the impeller tip with an absolute velocity of V2 that will have a tangential or whirl component Vw2. Under ideal conditions, V2, would be such that the whirl component is equal to the impeller speed U2 at the tip. Since air enters the impeller in axial direction, Vwl=0. Under the situation of Vwl=0 and Vw2=U2, we can derive from Eq. (15.2), the energy transfer per unit mass of air as

                                                        (16.1)
Due to its inertia the air trapped between the impeller vanes is reluctant to move round with the impeller and we have already noted that this results in a higher static pressure on the leading face of a vane than on the trailing face. It also prevents the air acquiring a whirl velocity equal to impeller speed. This effect is known as slip. Because of slip, we obtain Vw2 < U2. The slip factor s is defined in the similar way as done in the case of a centrifugal pump as

The value of s lies between 0.9 to 0.92. The energy transfer per unit mass in case of slip becomes

                                                  (16.2)

 

Diffuser
The basic purpose of a compressor is to deliver air at high pressure required for burning fuel in a combustion so that the burnt products of combustion at high pressure and temperature are used in turbines or propelling nozzles (in case of am aircraft engine) to develop mechanical power. The problem of designing an efficient combustion chamber is eased if velocity of the air entering the combustion chamber is as low as possible. It is necessary, therefore to design the diffuser so that only a small part of the stagnation temperature at the compressor outlet corresponds to kinetic energy.
It is much more difficult to arrange for an efficient deceleration of flow than it is to obtain efficient acceleration. There is a natural tendency in a diffusing process for the air to break away from the walls of the diverging passage and reverse its direction. This typically due to the phenomenon of boundary layer separation as explained section 9.6. This is shown in Fig. 16.7. Experiments have shown that the maximum permissible included angle of divergence is 11° to avoid considerable losses due to flow separation.
In order to control the flow of air effectively and carry-out the diffusion process in as short a length as possible, the air leaving the impeller is divided into a number of separate streams by fixed diffuser vanes. Usually the passages formed by the vanes are of constant depth, the width diverging in accordance with the shape of the vanes. The angle of the diffuser vanes at the leading edge must be designed to suit the direction of the absolute velocity of the air at the radius of the leading edges, so that the air will flow smoothly over vanes. As there is a radial gap between the impeller tip and the leading edge of the vanes (Fig. 16.8), this direction will not be that with which the air leaves the impeller tip.
To find the correct angle for diffuser vanes, the flow in the vaneless space should be considered. No further energy is supplied to the air after it leaves the impeller. If we neglect the frictional losses, the angular momentum  remains constant.
Hence  decreases from impeller tip to diffuser vane, in inverse proportion to the radius. For a channel of constant depth, the area of flow in the radial direction is directly proportional to the radius. The radial velocity  will therefore also decrease from impeller tip to diffuser vane, in accordance with the equation of continuity. If both  and  decrease from the impeller tip then the resultant velocity V decreases from the impeller tip and some diffusion takes place in the vaneless space. The consequent increase in density means that will not decrease in inverse proportion to the radius as done by , and the way varies must be found from the equation of continuity.

Lecture-8
Losses in a Centrifugal Compressor

 

The losses in a centrifugal compressor are almost of the same types as those in a centrifugal pump described in section 15.3.3 of Chapter 15. However, the following features are to be noted.

Frictional losses: A major portion of the losses is due to fluid friction in stationary and rotating blade passages. The flow in impeller and diffuser is decelerating in nature. Therefore the frictional losses are due to both skin friction and boundary layer separation.  The losses depend on the friction factor, length of the flow passage and square of the fluid velocity. The variation of frictional losses with mass flow is shown in Fig. 16.9.

Incidence losses: During the off-design conditions, the direction of relative velocity of fluid at inlet does not match with the inlet blade angle and therefore fluid cannot enter the blade passage smoothly by gliding along the blade surface. The loss in energy that takes place because of this is known as incidence loss. This is sometimes referred to as shock losses. However, the word shock in this context should not be confused with the aerodynamic sense of shock which is a sudden discontinuity in fluid properties and flow parameters that arises when a supersonic flow decelerates to a subsonic one as described in Chapter 14.

Clearance and leakage losses: Certain minimum clearances are necessary between the impeller shaft and the casing and between the outlet periphery of the impeller eye and the casing. The leakage of gas through the shaft clearance is minimized by employing glands. The clearance losses depend upon the impeller diameter and the static pressure at the impeller tip. A larger diameter of impeller is necessary for a higher peripheral speed and it is very difficult in the situation to provide sealing between the casing and the impeller eye tip.
The variations of frictional losses, incidence losses and the total losses with mass flow rate are shown in Fig. 16.9. The leakage losses comprise a small fraction of the total loss. The incidence losses attain the minimum value at the designed mass flow arte. The shock losses are, in fact zero at the designed flow arte. However, the incidence losses, as shown in Fig. 16.9, comprises both shock losses and impeller entry loss due to a change in the direction of fluid flow from axial to radial direction in the vaneless space before entering the impeller blades. The impeller entry loss is similar to that in a pipe bend and is very small compared to other losses. This is why the incidence losses show a non zero minimum value (Fig. 16.9) at the designed flow rate.

Compressor characteristics
The theoretical and actual head-discharge relationships of a centrifugal compressor are same as those of a centrifugal pump as described in Chapter 15. Therefore the curves of H-Q are similar to those of Figs. 15.26 and 15.27. However, the performance of a compressor is usually specified by curves of delivery pressure and temperature against mass flow rate for various fixed values of rotational speed at given values of inlet pressure and temperature. It is always advisable to plot such performance characteristic curves with dimensionless variables. To find these dimensionless variables, we start with a implicit functional relationship of all the variables as
                                            (16.9)

Where D= characteristic linear dimension of the machine, N= rotational, m= mass flow rate, = stagnation pressure at compressor inlet, = stagnation pressure at compressor outlet, = stagnation temperature at compressor inlet, = stagnation temperature at compressor outlet, and R= characteristics gads constant.
By making use of Buckingham’s p theorem, we obtain the non-dimensional groups (p terms) as

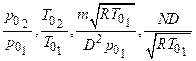
The third and fourth non-dimensional groups are defined as ‘non-dimensional mass flow’ and ‘non-dimensional rotational speed’ respectively. The physical interpretation of these two non-dimensional groups can be ascertained as follows.

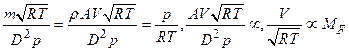
Therefore, the ‘non-dimensional mass flow’ and ‘non-dimensional rotational speed’ can be regarded as flow Mach number,  and rotational speed Mach number, .
When we are concerned with the performance of a machine of fixed size compressing a specified gas, and D may be omitted from the groups and we can write

Function                             (16.10)
Though the terms  and  are truly not dimensionless, they are referred as ‘non-dimensional mass flow’ and ‘non-dimensional rotational speed’ for practical purpose. The stagnation pressure and temperature ratios  and  are plotted against in the form of two families of curves, each curve of a family being drawn for fixed values of. The two families of curves represent the compressor characteristics. From these curves, it is possible to draw the curves of isentropic efficiency  for fixed values of. We can recall, in this context, the definition of the isentropic efficiency as
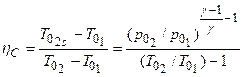                                             (16.11)

Before describing a typical set of characteristics, it is desirable to consider what might be expected to occur when a valve placed in the delivery line of the compressor running at a constant speed, is slowly opened. When the valve is shut and the mass flow rate is zero, the pressure ratio will have some value. A (Fig. 16.10), corresponding to the centrifugal pressure head produced by the action of the impeller on the air trapped between the vanes. As the valve is opened, flow commences and diffuser begins to influence the pressure rise, for which the pressure ratio increases. At some point B, efficiency approaches its maximum and the pressure ratio also reaches its maximum. Further increase of mass flow will result in a fall of pressure ratio. Foe mass flows greatly in excess of that corresponding to the design mass flow, the air angles will be widely different from the vane angles and breakaway of the air will occur. In this hypothetical case, the pressure ratio drops to unity at C, when the valve is fully open and all the power is absorbed in overcoming internal frictional resistances.
In practice, the operating point A could be obtained if desired but a part of the curve between A and B could not be obtained due to surging. It may be explained in the following way. If we suppose that the compressor is operating at a point D on the part of characteristics curve (Fig. 16.10) having a positive sloe, then a decrease in mass flow will be accompanied by a fall in delivery pressure. If the pressure of the air downstream of the compressor does not fall quickly enough, the air will tend to reverse its direction and will flow back in the direction of the resulting pressure gradient. When this occurs, the pressure ratio drops rapidly causing a further drop in mass flow until the point A is reached, where the mass flow is zero. When the pressure downstream of the compressor has reduced sufficiently due to reduced mass flow rate, the positive flow becomes established again the compressor picks up to repeat the cycle of events which occurs at high frequency.
This surging of air may not happen immediately the operating point moves to the left of B because the pressure downstream of the compressor may at first fall at a greater rate than the delivery pressure. As the mass flow is reduced, the reverse will apply and the conditions are unstable between A and B. As long as the operating point is on the part of the characteristics having a negative slope, however, decrease in mass flow is accompanied by a rise in delivery pressure and the operation is stable.
Let us consider the constant speed curve ABC (Fig. 16.10). There is an additional limitation to the operating range, between B and C. As the mass flow increases and the pressure decreases, the density is reduced and the radial component of velocity must increase. At constant rotational speed this means an increase in resultant velocity and hence in angle of incidence at the diffuser vane leading edge. At some point say E, the position is reached where no further increase in mass flow can be obtained no matter how wide open the control valve is. This point represents the maximum delivery obtainable at the particular rotational speed for which the curve is drawn. This indicates that at some point within the compressor sonic conditions have been reached, causing the limiting maximum mass flow rate to be set as in the case of compressible flow through a converging diverging nozzle. Choking is said to have taken place. Other curves may be obtained for different speeds, so that the actual variation of pressure ratio over the complete range of mass flow and rotational speed will be shown by curves such as those in Fig. 16.11. The left hand extremities of the constant speed curves may be joined up to form surge line, the right hand extremities indicate choking (Fig. 16.11).

 

Lecture-16
A brief note on Gas Turbine combustors

Over a period of five decades, the basic factors influencing the design of combustion systems for gas turbines have not changed, although recently some new requirements have evolved. The key issues may be summarized as follows.

• The temperature of the gases after combustion must be comparatively low to suit the highly stressed turbine materials. Development of improved materials and methods of blade cooling, however, has enabled permissible combustor outlet temperatures to rise from about 110K to as much as 1850 K for aircraft applications.
• At the end of the combustion space the temperature distribution must be of known form if the turbine blades are not to suffer from local overheating. In practice, the temperature can increase with radius over the turbine annulus, because of the strong influence of temperature on allowable stress and the decrease of blade centrifugal stress from root to tip.
• Combustion must be maintained in a stream of air moving with a high velocity in the region of 30-60 m/s, and stable operation is required over a wide range of air/fuel ratio from full load to idling conditions. The air/fuel ratio might vary from about 60:1 to 120:1 for simple cycle gas turbines and from 100:1 to 200:1 if a heat-exchanger is used. Considering that the stoichiometric ratio is approximately 15:1 it is clear that a high dilution is required to maintain the temperature level dictated by turbine stresses
• The formation of carbon deposits (‘coking’) must be avoided, particularly the hard brittle variety. Small particles carried into the turbine in the high-velocity gas stream can erode the blades and block cooling air passages; furthermore, aerodynamically excited vibration in the combustion chamber might cause sizeable pieces of carbon to break free resulting in even worse damage to the turbine.
• In aircraft gas turbine, combustion must also be stable over a wide range of chamber pressure because of the substantial change in this parameter with a altitude and forward speed. Another important requirement is the capability of relighting at high altitude in the event of an engine flame-out.
• Avoidance of smoke in the exhaust is of major importance for all types of gas turbine; early jet engines had very smoky exhausts, and this became a serious problem around airports when jet transport aircraft started to operate in large numbers. Smoke trails in flight were a problem for military aircraft, permitting them to be seen from a great distance. Stationary gas turbines are now found in urban locations, sometimes close to residential areas.
• Although gas turbine combustion systems operate at extremely high efficiencies, they produce pollutants such as oxides of nitrogen (NOx), carbon monoxide (CO) and unburned hydrocarbons (UHC) and these must be controlled to very low levels. Over the years, the performance of the gas turbine has been improved mainly by increasing the compressor pressure ratio and turbine inlet temperature (TIT). Unfortunately this results in increased production of NOx. Ever more stringent emissions legislation has led to significant changes in combustor design to cope with the problem.

 

Probably the only feature of the gas turbine that eases the combustion designer’s problem is the peculiar interdependence of compressor delivery air density and mass flow which leads to the velocity of the air at entry to the combustion system being reasonably constant over the operating range.
For aircraft applications there are the additional limitations of small space and low weight, which are, however, slightly offset by somewhat shorter endurance requirements. Aircraft engine combustion chambers are normally constructed of light-gauge, heat-resisting alloy sheet (approx. 0.8 mm thick), but are only expected to have a life of some 10000 hours. Combustion chambers for industrial gas turbine plant may be constructed on much sturdier lines but, on the other hand, a life of about 100000 hours is required. Refractory linings are sometimes used in heavy chambers, although the remarks made in (d) about the effects of hard carbon deposits breaking free apply with even greater force to refractory material.

Aircraft Engines and Propulsion System

The following four types of aircraft engines are generally used

• Turbojet Engine
• Turboprop Engine
• Turbofan Engine
• Ramjet Engine

1. Turbojet Engine

The turbojet engine consists of a gas turbine, the output of which is used solely to provide power to the compressor. The compressor and the turbine are normally mounted on common shaft. Air is taken into the engine through an approximate diffuser duct, passes through the compressor and enters the combustions chamber, where it is mixed and burned with fuel.
Most common fuels are hydrocarbons (Aviation kerosene). The ratio of fuel to air is determined by the maximum allowable gas temperature permitted by the turbine. Normally, a considerable excess air is used. The hot high pressure gases are then expended through the turbine to a pressure which is higher than the ambient atmosphere, and yet sufficiently lower than the combustion chamber pressure, to produce just enough power in the turbine to run the compressor. After leaving the turbine, the gas is expanded to the ambient pressure through an appropriate nozzle. As this occurs, the gas is accelerated to a velocity, which is greater than the incoming velocity of the ingested air, and therefore produces a propulsive thrust.

2. Turboprop Engine

In this engine, a higher proportion of the total available pressure drop from the combustion chamber to the atmosphere is taken through the turbine and a smaller proportion through the propulsive nozzle. This strategy produces excess power in the turbine. The excess power is used not only to derive the compressor, but also a drive a propeller, in the same way as in the conventional reciprocating engines.

3. Turbofan Engine

This is another variety of gas-turbine aircraft engine. This is very similar to the turboprop in principle, except that a fan is used instead of a propeller, and this fan is contained within a duct as shown in the above figure.

4. Ramjet Engine

At higher forward speeds, the ram pressure of the air is already very large, and the necessity for a compressor tends to disappear. A turbojet engine minus the compressor and turbine, but with a combustion chamber, is known as a ramjet engine. Such engines simply consists of

1. A duct designed to diffuse the incoming air, slowing its velocity and raising its pressure
2. A combustor, designed to heat the air, normally by combustion with a liquid fuel
3. A nozzle, designed to expand and accelerate the now heated gases rearwards

The ramjet engine does not accelerate itself from a standing start but required some other form of propulsion, usually a rocket, to accelerate it to near its operating speed.

PROBLEMS AND SOLUTIONS FOR CENTRIFUGAL COMPRESSORS

Exercises
[For al the Exercises, assume R=287J/kg K and  l= 1.4 for air]

16.1 Determine the pressure ratio developed and the specific work input to drive a centrifugal air compressor having an impeller diameter of 0.5 m and running at 7000 rpm. Assume zero whirl at the entry and T1t = 288 K.
(1.47,33.58 kJ/kg)

16.2 A centrifugal compressor develops a pressure ratio of 4:1. The inlet eye of the compressor impeller is 0.3 m in diameter. The axial velocity at inlet is 120 m/s and the mass flow rate is 10 kg/s. The velocity in the delivery duct is 110 m/s. The tip speed of the impeller is 450 m/s and runs at 16,000 rpm with a total head isentropic efficiency of 80%. The inlet stagnation temperature and pressure are 101 kN/m2 and 300 K. Calculate (a) the static temperatures and pressures at inlet and outlet of the compressor, (b) the static pressure ratio, (c) the power required to drive the compressor.
Ans. (T1 = 292.8 K, T2 = 476.45 K, p = 93 kN/m2,
p2 = 386.9 kN/m2, p2/p1 = 4.16, p = 1.83 MW)

16.3 The following results were obtained from a test on a small single-sided centrifugal compressor
Compressor delivery stagnation pressure                                   2.97 bar
Compressor delivery stagnation temperature                  429 K
Static pressure at impeller tip                                          1.92 bar
Mass flow                                                                        0.60 kg/s
Rotational speed                                                              766 rev/s
Ambient conditions                                                         0.99 bar 288 K
Determine the isentropic efficiency of the compressor.
The diameter of the impeller is 0.165 m, the axial depth of the vaneless diffuser is 0.01m and the number of impeller vanes is 17. Making use of the Stanitz equation for slip factor, calculate the stagnation pressure at the impeller tip.
Ans. (0.76, 3.13 bar)

16.4 A single sided centrifugal compressor is to deliver 14 kg/s of air when operating at a pressure ratio of 4:1 and a speed of 200 rev/s. The inlet stagnation conditions are 288 K and 1.0 bar. The slip factor and power input factor may be taken as 0.9 and 1.04 respectively. The overall isentropic efficiency is 0.80. Determine the overall diameter of the impeller.
Ans. (0.67m)

PROBLEMS ON AXIAL COMPRESSORS

16.5 Each stage of an axial flow compressor is of 50% degree of reaction and has the same mean blade speed and the same value of outlet relative velocity angle b2=30°. The mean flow coefficiency (Vf/U) is constant for all stages at 0.5. At entry to the first stage, the stagnation temperature is 290 K, the stagnation pressure is 101 kPa. The static pressure is 87 kPa and the flow area is 0.38 m2. Determine the axial velocity, the mass flow rate and the shaft power needed to derive the compressor when there are 6 stages and the mechanical efficiency is 0.98.
Ans. (135.51 m/s, 56.20 kg/s, 10.68 MW)

16.6 An axial flow compressor stage has blade root, mean and tip velocities of 150, 200 and 250 m/s The stage is to be designed for a stagnation temperature rise of 20 K and an axial velocity of 150 m/s, both constant from root to tip. The work done factor is 0.93. Assuming degree of reaction 0.5 at mean radius, determine the stage air angles at root mean and tip for a free vortex design where the whirl component of velocity varies inversely with the radius
Ans. (a1 = 17.04° (= b2), b1 = 45.75° (= a2) at mean radius; a1 = 13.77°,
b1 = 54.88°, b2 = 40.36°, a2 = 39.34°  at tip; a1 = 22.10°,
b1 = 30.71°, b2 = -19.95°, a2 = 53.74°  at root)

16.7 An axial compressor has the following data:

Temperature and pressure at entry                            300 K, 1.0 bar
Degree of reaction                                                     50%
Mean blade ring diameter                                          0.4 m
Rotational speed                                                        15,000 rpm
Blade height at entry                                                 0.08 m
Air angles at rotor and stator exit                              25°
Axial velocity                                                            150 m/s
Work done factor                                                       0.90
Isentropic stage efficiency                                         85%
Mechanical efficiency                                                           97%

Determine (a) air angles at the rotor and stator entry (b) the mass flow rate of air (c) the power required to derive the compressor, (d) the pressure ratio developed by the stage (e) Mach number (based on relative velocities) at the rotor entry.
Ans. [(a) 25°, 58.44° (b) 17.51 kg/s, (c) 0.89 MW, (d) 1.58, (e) 0.83]

16.8 An axial flow compressor .stage has a mean diameter of 0.6 m and runs at 15,000 rpm. If the actual temperature rise and pressure ratio developed are 30°C and 1.36 respectively, determine (a) the power required to derive the compressor while delivering 57 kg/s of air. Assume mechanical efficiency of 86% and an initial temperature of 35°C (b) the isentropic efficiency of the stage and (c) the degree of reaction if the temperature at the rotor exit is 55°C.
Ans. [(a) 2 MW, (b) 94.2%, (c) 66.6%]