Students will often experience difficulty in handling problems involving two and three-dimensional geometrical constructions.
Copying a selection of these examples on the drawing board or on CAD equipment will certainly enable the reader to gain confidence. It will assist them to visualise and position the lines in space, which form each part of a view, or the boundary, of a three-dimensional object. It is a necessary part of draughtsmanship to be able to justify every line and dimension which appears on a drawing correctly.
Many software programs will offer facilities to perform a range of constructions, for example tangents, ellipses and irregular curves. Use these features where possible in the examples that follow.
Assume all basic dimensions where applicable.

To Bisect a Given Angle AOB

1. With centre O, draw an arc to cut OA at C and OB at D.

1. With centres C and D, draw equal radii to intersect at E.

3. Line OE bisects angle AOB.

Figure 1

To Bisect a Given Straight Line AB

1. With centre A and radius greater than half AB, describe an arc.

2. Repeat with the same radius from B, the arcs intersecting at C and D.
3. Join C to D and this line will be perpendicular to and bisect AB.

Figure 2

To Bisect a Given Arc AB

1. With centre A and radius greater than half AB, describe an arc.

2. Repeat with the same radius from B, the arcs intersecting at C and D.
3. Join C to D to bisect the arc AB.

Figure 3

To Find the Centre of a Given Arc AB

1. Draw two chords, AC and BD.

2. Bisect AC and BD as shown; the bisectors will intersect at E.
3. The centre of the arc is point E.

Figure 4

To Inscribe a Circle in a Given Triangle ABC

1. Bisect any two of the angles as shown so that the bisectors intersect at D.
2. The centre of the inscribed circle is point D.

Figure 5

To Circumscribe a Circle around Triangle ABC

1. Bisect any two of the sides of the triangle as shown, so that the bisectors intersect at D.

2. The centre of the circumscribing circle is point D.

Figure 6

To Draw a Hexagon, Given the Distance across the Corners

Method A

1. Draw vertical and horizontal centre lines and a circle with a diameter equal to the given distance.

2. Step off the radius around the circle to give six equally spaced points, and join the points to give the required hexagon.

Figure 7

Method B

1. Draw vertical and horizontal centre lines and a circle with a diameter equal to the given distance.

2. With a 60° set-square, draw points on the circumference 60° apart.
3. Connect these six points by straight lines to give the required hexagon.

Figure 8

To Draw a Hexagon, Given the Distance across the Flats

1. Draw vertical and horizontal centre lines and a circle with a diameter equal to the given distance.

2. Use a 60° set-square and tee-square as shown, to give the six sides.

Figure 9

To Draw a Regular Octagon, Given the Distance across Corners

Repeat the instructions in Figure 8 but use a 45° set-square, then connect the eight points to give the required octagon.

Figure 10

To Draw a Regular Octagon, Given the Distance across the Flats

Repeat the instructions in Figure 9 but use a 45° set-square to give the required octagon.

Figure 11

To Draw a Regular Polygon, Given the Length of the Sides

Note that a regular polygon is defined as a plane figure which is bounded by straight lines of equal length and which contains angles of equal size. Assume the number of sides is seven in this example.

1. Draw the given length of one side AB, and with radius AB describe a semi-circle.
2. Divide the semi-circle into seven equal angles, using a protractor, and through the second division from the left join line A2.
3. Draw radial lines from A through points 3, 4, 5, and 6.
4. With radius AB and centre on point 2, describe an arc to meet the extension of line A3, shown here as point F.
5. Repeat with radius AB and centre F to meet the extension of line A4 at E.

1. Connect the points as shown, to complete the required polygon.

Figure 12

Tangency

If a disc stands on its edge on a flat surface it will touch the surface at one point. This point is known as the point of tangency, as shown in Figure 13 and the straight line which represents the flat plane is known as a tangent. A line drawn from the point of tangency to the centre of the disc is called a normal, and the tangent makes an angle of 90° with the normal.
The following constructions show the methods of drawing tangents in various circumstances.

Figure 13

To Draw a Tangent to a Point A on the Circumference of a Circle, Centre O

Join OA and extend the line for a short distance. Erect a perpendicular at point A by the method shown.

Figure 14

To Draw a Tangent to a Circle from any Given Point A Outside the Circle

Join A to the centre of the circle O. Bisect line AO so that point B is the mid-point of AO. With centre B, draw a semi-circle to intersect the given circle at point e. Line AC is the required tangent.

Figure 15

To Draw an External Tangent to Two Circles

Join the centres of the circles by line AB, bisect AB, and draw a semi-circle. Position point E so that DE is equal to the radius of the smaller circle. Draw radius AE to cut the semi-circle at point G. Draw line AGH so that H lies on the circumference of the larger circle. Note that angle AGB lies in a semi-circle and will be 90°. Draw line HJ parallel to BG. Line HJ will be tangential to the two circles and lines BJ and AGH are the normals.

Figure 16

To Draw an Internal Tangent to Two Circles

Join the centres of the circles by line AB, bisect AB and draw a semi-circle. Position point E so that DE is equal to the radius of the smaller circle BC. Draw radius AE to cut the semi-circle in H. Join AH; this line crosses the larger circle circumference at J. Draw line BH. From J draw a line parallel to SH to touch the smaller circle at K. Line JK is the required tangent. Note that angle AHB lies in a semi-circle and will therefore be 90°. AJ and BK are normals.

Figure 17

To Draw Internal and External Tangents to Two Circles of Equal Diameter

Join the centres of both circles by line AB. Erect perpendiculars at points A and B to touch the circumferences of the circles at points C and D. Line CD will be the external tangent. Bisect line AB to give point E, then bisect BE to give point G. With radius BG, describe a semi-circle to cut the circumference of one of the given circles at H. Join HE and extend it to touch the circumference of the other circle at J. Line HEJ is the required tangent. Note that again the angle in the semi-circle, BHE, will be 90°, and hence BH and AJ are normals.

Figure 18

To Draw a Curve of Given Radius to Touch Two Circles when the Circle are Outside the Radius

Assume that the radii of the given circles are 20 and 25 mm, spaced 85 mm apart, and that the radius to touch them is 40 mm.
With centre A. describe an arc equal to 20 + 40 = 60 mm.
With centre B, describe an arc equal to 25 + 40 = 65 mm.
The above arcs intersect at point C. With a radius of 40 mm, describe an arc from point C as shown, and note that the points of tangency between the arcs lie along the lines joining the centres AC and BC. It is particularly important to note the position of the points of tangency before lining in engineering drawings, so that the exact length of an arc can be established.

Figure 19

To Draw a Curve of Given Radius to Touch Two Circles when the Circles are Inside the Radius

Assume that the radii of the given circles are 22 and 26 mm, spaced 86 mm apart, and that the radius to touch them is 100 mm.
With centre A, describe an arc equal to 100 - 22 = 78mm.
With centre B, describe an arc equal to 100 - 26 = 74mm.
The above arcs intersect at point C. With a radius of 100 mm, describe an arc from point C, and note that in this case the points of tangency lie along line CA extended to D and along line CB extended to E.

Figure 20

To Draw a Radius to Join a Straight Line and a Given Circle

Assume that the radius of the given circle is 20 mm and that the joining radius is 22 mm.
With centre A, describe an arc equal to 20 + 22 = 42mm.
Draw a line parallel to the given straight line and at a perpendicular distance of 22 mm from it, to intersect the arc at point B.
With centre B, describe the required radius of 22 mm, and note that one point of tangency lies on the line AB at C; the other lies at point D such that BD is at 90° to the straight line.

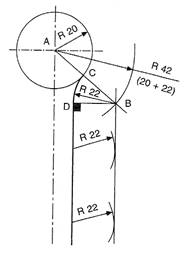
Figure 21

To Draw a Radius which is Tangential to Given Straight Lines

Assume that a radius of 25 mm is required to touch the lines shown in the figures. Draw lines parallel to the given straight lines and at a perpendicular distance of 25 mm from them to intersect at points A. As above, note that the points of tangency are obtained by drawing perpendiculars through the point A to the straight lines in each case.

Figure 22