Furnace Temperatures

An important auxiliary to a furnace is some method of measuring its temperature, because the successful heat treatment of steel depends on close adherence to the correct temperature. There are many methods used for this, a simple one being to put in the furnace some substance which melts at the temperature it is desired to verify. The substances used for this are moulded in the form of cones from mixtures of Kaolin, lime, feldspar, magnesia, quartz and boric acid, with their melting temperatures arranged in steps from 600°C to 2000 °C. When a furnace temperature is required, several of these cones, covering a range of melting temperatures within which the temperature of the furnace is judged to lie, are put in and observed. The temperature is then judged from which cones collapse, and which remain unaffected by the heat of the furnace. For example, to verify a temperature judged to be 810°-820°C, cones having melting points of 790, 815 and 835°C might be put in, the temperature then being estimated from their condition after sufficient time had elapsed for them to be affected. These cones are called Seger Cones or Sentinels and Figure 1 shows how they appear after a test.

Figure 1 - Seger Cones after being in Furnace

Strength of Materials

Mechanical Testing

Designers and engineers need to know how metals are going to perform when they are used. Special tests have been developed to test for mechanical properties, such as:

• Strength
  
• Ductility
  
• Hardness
  
• Toughness
  
• Fatigue

 

These tests are used for both standardisation and checking of quality.

Tensile Testing

A metal which can be drawn out into a thin wire is said to be ductile. Ductility of a metal can be found by using an extensometer. Many types of extensometer exist. Any extensometer has two basic parts:

• some method of applying a pull to the test piece (specimen) and showing how much of a load is applied
  
• a method of measuring the amount the specimen stretches or extends during the test.

 

Specimen pieces of metal are made to suit the machine being used because machines have different ways of holding the pieces.

These specimen pieces may be rectangular or circular, but must have a standard cross-sectional area, and also have marks 50mm apart.

Figure 2 - Tensile Strength Specimens

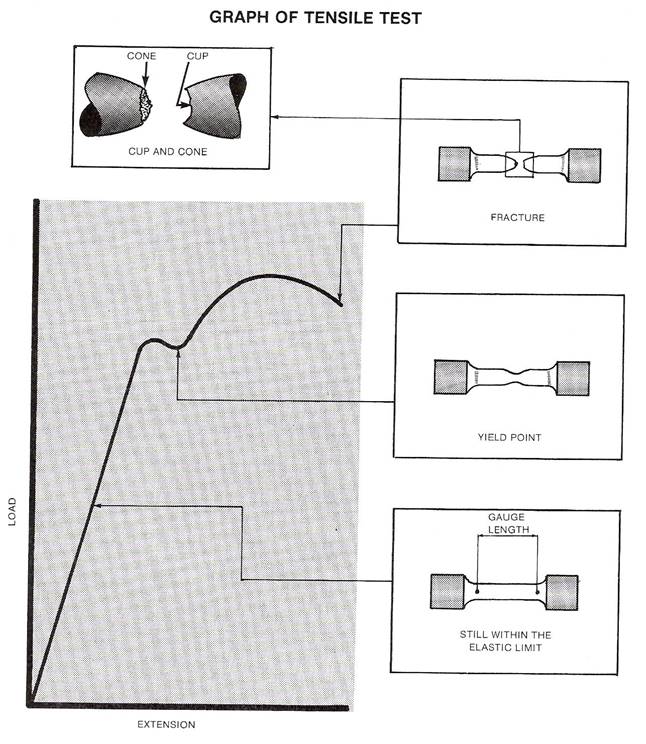
Figure 3 - Graph of Tensile Test

Strain

E.G.    A steel bar which was 4 metres long is stretched by 6mm. Find the strain.

Extension = Change in Length = 0.006m
Original Length = 4m

Strain  =    =  0.0015 or 1.5 x 10

Stress

When a load or force is applied to a piece of metal, the load is carried by the whole area of cross section. In other words, each unit of area carries an equal amount of load.
It is the amount of load or force carried by a unit area that is called stress.

E.G.    If a steel bar of diameter 8mm has got a pull of 402N, find the stress in the bar.

Cross-Sectional Area = 0.785 x D²
= 0.785 x 64 mm²
= 50.24 mm²
Load = 402 N
So Stress         =    =  8 N/mm²

Modulus of Elasticity

In the elastic range of a material, stress is directly propor­tional to strain, which is another way of stating Hooke's Law.
So,  will be constant for each material.
The constant is called Young's Modulus of Elasticity, where
Young's Modulus of Elasticity (E) =

E.G.    In a tensile test on a non-ferrous alloy, the test piece had a gauge length of 50mm, and a diameter of 10mm. If, in the middle of its elastic range, a load of 20 kN produced an extension of 0.1mm, find Young's Modulus of Elasticity.

Cross-sectional area = 0.785 x D² = 78.5mm²
Stress  =    =  0.255kN/mm²

So, Young's Modulus of Elasticity  = 
= 127.5 kN/mm²

(1 kN = 1000N and 1m² = 1,000,000 mm²)
So, 127.5 kN/mm² = 127.5 x 10  N/m²

This is the way E is usually expressed. Young's Modulus gives an indication of the stiffness of the material. The value of E can be the same in compression as in tension for some materials, but this is not always so.

Tensile Strength

Tensile strength is the maximum force or load applied to the specimen before it fractures, divided by the original cross-sectional area.

Tensile strength is sometimes called Ultimate Tensile Strength.

Ductility

An indication of the ductility of the metal used in the test is given by percentage elongation.

Sometimes the reduction in area is used for ductility.

Many materials such as hardened steel or non ferrous metals have no well defined yield point, so the proof stress is used. The yield point is more important than the tensile strength and a stress which gives a certain amount of extension is specified. This specified stress is known as proof stress. Figure 4 shows how the figure is arrived at.

Shear Strength

A shear force tends to shear the material into two parts. Shear force is used in cutting with scissors, tinsnips, guillotine and in 'punching' or piercing with a press. Figure 5 shows a bar of metal being sheared.

E.G.    If the bar in Figure 4 has a cross-sectional area of 60mm² and the metal it is made from has a shear strength of 210 N/mm², what force is necessary to shear the bar?

Cross-sectional area of bar    = 60mm²
Shear strength of metal          = 210N/mm²
Force required                                   = 60 x 210N
= 12600N
or 12.6kN

Figure 4 - Proof Stress

Figure 5 - Forces Experienced by Materials

Compressive Strength

This is the strength of the material in compression and is calculated from:

Factor of Safety

When an engineer designs a component, the stress which the component will be subjected to is taken into account. The dimensions necessary to withstand the stress are calculated. If these exact figures were used, failure of the component could occur due to either an increase in load or a deterioration of the material. This is why it is the practice to make the components capable of withstanding much greater loads than their safe working loads.

E.G.    Supposing a component is to withstand a load of 50kN, but it is designed so that it can withstand 200kN.
Here, the factor of safety, as it is called, is equal to 4 as shown below:
Safe working load      = 50kN
Maximum load           = 200kN
Factor of safety          = 200/50 = 4