Figure 1 shows three views of a cube in orthographic projection; the phantom line indicates the original position of the cube, and the full line indicates the position after rotation about the diagonal AB. The cube has been rotated so that the angle of 45 ° between side AC1 and diagonal AB now appears to be 30° in the front elevation, C1 having been rotated to position C. It can clearly be seen in the end view that to obtain this result the angle of rotation is greater than 30°. Also, note that, although DF in the front elevation appears to be vertical, a cross check with the end elevation will confirm that the line slopes, and that point F lies to the rear of point D. However, the front elevation now shows a three dimensional view, and when taken in isolation it is known as an isometric projection.

Figure 1 - Cube in Orthographic Projection

This type of view is commonly used in pictorial presentations, for example in car and motor-cycle service manuals and model kits, where an assembly has been 'exploded' to indicate the correct order and position of the component parts. It will be noted that, in the isometric cube, line AC1 is drawn as line AC, and the length of the line is reduced.
Figure 2 shows an isometric scale, which in principle is obtained from lines at 45° and 30° to a horizontal axis. The 45° line XY is calibrated in millimetres commencing from point X, and the dimensions are projected vertically on to the line XZ. By similar triangles, all dimensions are reduced by the same amount, and isometric lengths can be measured from point X when required. The reduction in length is in the ratio
isometric length   =    cos 45°    =     0.7071
true length            cos 30°            0.8660
=   0.8165

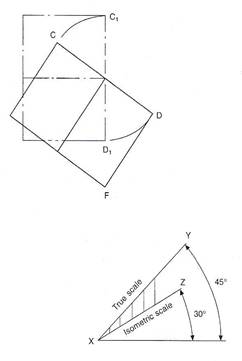
Figure 2 - Isometric Scale

Now, to reduce the length of each line by the use of an isometric scale is an interesting academic exercise, but commercially an isometric projection would be drawn using the true dimensions and would then be enlarged or reduced to the size required.

Note that, in the isometric projection, lines AE and DB are equal in length to line AD; hence an equal reduction in length takes place along the apparent vertical and the two axes at 30° to the horizontal. Note also that the length of the diagonal AB does not change from orthographic to isometric, but that of diagonal C1D1 clearly does. When setting out an isometric projection, therefore, measurements must be made only along the isometric axes EF, DF, and GF.

Figure 3 shows a wedge, which has been produced from a solid cylinder, and dimensions A, E,and C indicate typical measurements to be taken along the principal axes when setting out the isometric projection. Any curve can be produced by plotting a succession of points in space after taking ordinates from the X, Y, and Z axes.

 

Figure 3 - Construction Principles for Points in Space, with Complete Solution

Figure 4(a) shows a cross-section through an extruded alloy bar: the views (b), (c), and (d) give alternative isometric presentations drawn in the three principal planes of projection. In every case, the lengths of ordinates OP, OQ, P1, and Q2, etc. are the same, but are positioned either vertically or inclined at 30° to the horizontal.

Figure 4 - Views (b), (c) and (d) are Isometric Projections of the Section in View (a)

Figure 5 shows an approximate method for the construction of isometric circles in each of the three major planes. Note the position of the points of intersection of radii RA and RB.

Figure 5 - Construction of Isometric Circles

The construction shown in Figure 5 can be used partly for producing corner radii. Figure 6 shows a small block with radiused corners together with isometric projection, which emphasises the construction to find the centres for the corner radii; this should be the first part of the drawing to be attempted. The thickness of the block is obtained from projecting back these radii a distance equal to the block thickness and at 30°. Line in those parts of the corners visible behind the front face, and complete the pictorial view by adding the connecting straight lines for the outside of the profile.

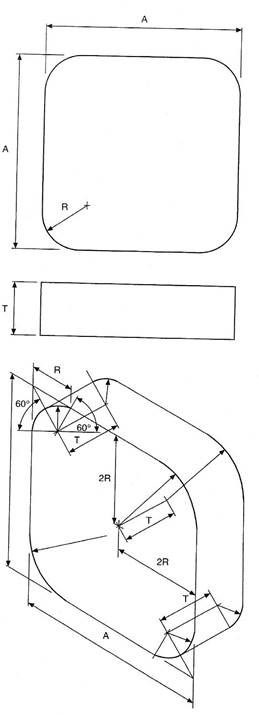
Figure 6 - Isometric Constructions for Corner Radii

In the approximate construction shown, a small inaccuracy occurs along the major axis of the ellipse, and Figure 7 shows the extent of the error in conjunction with a plotted circle. In the vast majority of applications where complete but small circles are used, for example spindles, pins, parts of nuts, bolts, and fixing holes, this error is of little importance and can be neglected.

 

 

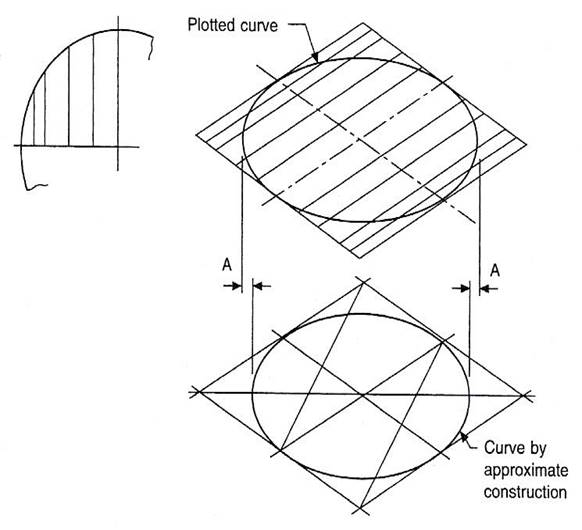
Figure 7 - Relationship between Plotted Points and Constructed Isometric Circles

Oblique Projection

Figure 8 shows part of a plain bearing in orthographic projection, and Figure 9 show alternative pictorial projections.

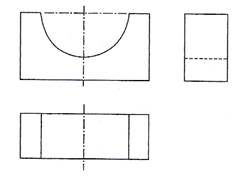
Figure 8 - Plain Bearing in Orthographic Projection

It will be noted in Figure 9 that the thickness of the bearing has been shown by projecting lines at 45° back from a front elevation of the bearing. Now, the picture on the right of Figure 9 conveys the impression that the bearing is thicker than the true plan suggests, and therefore in the picture to the left of Figure 9 the thickness has been reduced to one half of the actual size. The picture on the left of Figure 9 is known as an oblique projection, and objects, which have curves in them, are easiest to draw if they are turned, if possible, so that the curves are presented in the front elevation. If this proves impossible or undesirable, then Figure 10 shows part of the ellipse, which results from projecting half sizes back along the lines inclined at 45°.

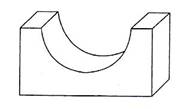
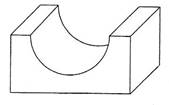
Figure 9 - Alternative Pictorial Projects

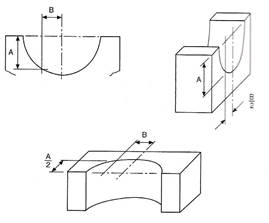
Figure 10 - Part of the Ellipse

A small die-cast lever is shown in Figure 11, to illustrate the use of a reference plane. Since the bosses are of different thicknesses, a reference plane has been taken along the side of the web; and, from this reference plane, measurements are taken forward to the boss faces and backwards to the opposite sides. Note that the points of tangency are marked, to position the slope of the web accurately.
With oblique and isometric projections, no allowance is made for perspective, and this tends to give a slightly unrealistic result, since parallel lines moving back from the plane of the paper do not converge.

Figure 11 - Die-Cast Lever

Further information regarding pictorial representations, reference can be made to BS EN ISO 5456-3. The Standard contains details of Dimetric, Trimetric, Cavalier, Cabinet, Planometric and Perspective projections.

Isometric Drawing

Isometric drawing is a form of pictorial drawing based on lines at 30 degrees from the horizontal. Figure 12 shows the basic idea when making an isometric drawing of a rectangular prism. Vertical lines are drawn with the aid of the right angle of a set square, lines at 30 degrees are drawn with the aid of a 30,60 set square.

When constructing an isometric drawing, all measurements must be made along the isometric axes - either the vertical lines or along the 30 degree lines. This applies even when constructing arcs or curved lines in isometric drawings. Figure 13 shows the method of finding the sizes along the isometric axes for the construction of Figure 14. Figure 15 shows how lines, which are not along the isometric axes, must be constructed from measurements taken along the axes.

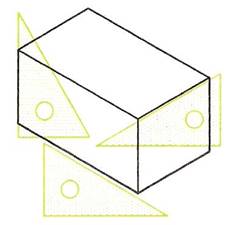
Figure 12 - Isometric Drawing of a Rectangular Prism

Figure 13 - Sizes must be taken along Isometric Axes

Figure 14 - Finished Isometric Drawing to the Sizes in Figure 13

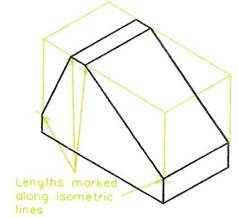
Figure 15 - Sloping Lines - Sizes must be measured along Axes

Constructing Isometric Curves

Figure 16 shows how an isometric circle is constructed:

1. Draw a circle of the required diameter - the lower drawing of Figure 16. Draw vertical lines - a, b and c - at any spacings across the circle.

2. Draw the two centre lines for the circle at 30 degrees each way - the upper drawing of Figure 16.
3. Mark off the lengths Oa, Ob and Oc, taken from the circle, along one of the isometric centrelines, each side of the centre O. Draw 30 degree lines through the points a, band c.
4. Each side of the centre line from a, b and c mark off the lengths a1, b2 and c3 along the 30 degree lines from a, b and c.
5. Mark the lengths Od each side along the centre line in the isometric drawing.
6. All necessary points for drawing the isometric circle have now been found. Draw a fair curve through the points to complete the required isometric circle - which is an ellipse.

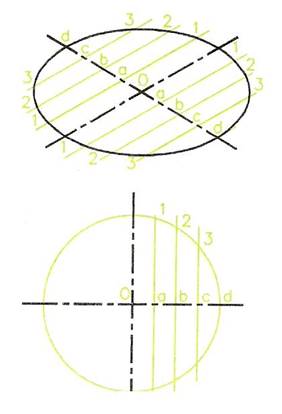
Figure 16 - Method of Constructing an Isometric Circle

Figure 17 shows a similar construction for circles in other isometric positions.

Figure 17 - Other Positions for Isometric Circles

Figure 18 is an example of a simple isometric drawing and Figure 19 another example which includes isometric 'circles'.

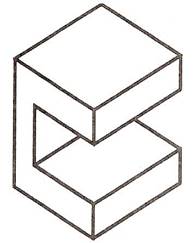
Figure 18 - Simple Isometric Drawing

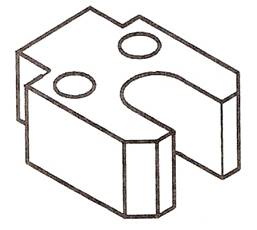
Figure 19 - Simple Isometric Drawing Involving Circles

Note: The reader is advised not to use isometric ellipse templates until he or she has had sufficient practise in constructing isometric ellipses as shown above.

Exploded Isometric Drawing

A Simple Exploded Isometric Drawing

Figure 20 is a simple ‘exploded’ isometric drawing; its parts have been ‘exploded’ along the isometric axes.

Figure 20 - Simple Exploded Isometric Drawing

An Exploded Isometric Drawing

Figure 21 is an exploded isometric drawing of a fork end, showing the two parts – its end piece and its rodin an exploded position. The rodis shown pulled out from the END along an isometric 30 degree axis. A rear view of the end pieceis included to show that the rodfits into a hole in its back face. To construct the drawing:

1. Working to the sizes given with Figure 21, draw the end piece, remembering that the chamfer sizes must be taken along the isometric lines.
2. Construct the rodusing the method shown in Figure 16 to draw the curves of the isometric circles.
3. Line in the required drawing outline and erase any unwanted lines.
4. Add a title block, which includes your name and the title EXPLODED ISOMETRIC DRAWING in 8 mm high capital letters.

Figure 21 - Exploded Isometric Drawing

Freehand Drawing

For preparing the layouts for orthographic drawings and for the necessary preparation work when designing, freehand drawing (or sketching) is a skill, which should be gained by practice. HB or B grade pencils are more suitable for freehand work than the 2H or 3H pencils, which are used for technical drawings made with the aid of instruments. If isometric and square grid papers are available, a good tip is to start learning how to draw freehand sketches on grid papers. Such grid papers can be purchased in A4 or A3 sheets with the grid lines printed in green or blue - either square grids or isometric grids are available. The spacing of the grid lines is either at 10 mm intervals or at 5 mm intervals. However, when you have gained sufficient skill in freehand drawing with the aid of grid papers, it is best to then sketch on plain paper without the grid lines. The examples given in this book are for freehand sketching on either the lines of orthographic projection or isometric drawing.
An example of a freehand drawing of a pedestal mounting as preparation for the layout of the drawing before constructing the views of an orthographic projection are shown in three examples - Figure 22 on an A3 sheet of 10 mm square grid paper, Figure 23 on a smaller sheet of grid paper and Figure 24 on plain paper without a grid. Figure 25 shows a freehand isometric drawing on isometric grid paper with the grid at 10 mm spacing. Figure 26 is a similar freehand drawing on isometric lines on plain paper without grid lines.

Figure 22 - Freehand Drawing on an A3 Sheet of 10mm Square Grid Paper

Figure 23 - Example of a Freehand Drawing on a 10mm Square Grid Paper

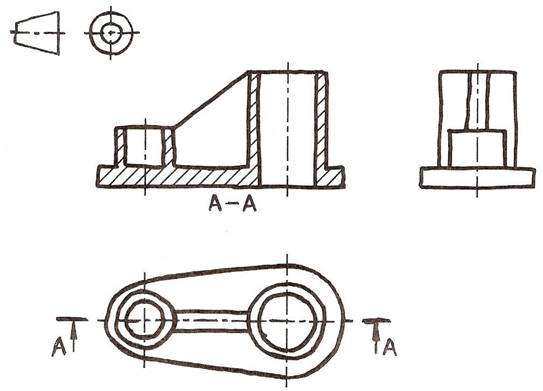
Figure 24 - Freehand Drawing of an Orthographic Projection on Plain Paper without Grid Lines

Figure 25 - Freehand Isometric Drawing on Isometric Grid Paper with Line Spacing at 10mm

 

Figure 26 - Freehand Drawing on Isometric Lines on Plain Paper without Grid Lines

The 4-Arcs Method of Drawing Isometric Circles

Figure 27 shows the method of drawing an isometric circle with the aid of instruments.

1. Draw the 30 degree lines which represent the square circumscribing the circle. Thus lines AB, BC, CD and DA are all at 30 degrees and are all the same length.

1. Draw the diagonal AC.

3. Draw BF and DE in which E is the centre point of AB and F is the centre point of CD.
4. With G, the intersection of AC and BF, as a centre, draw an arc of radius GF.
5. Draw an arc of centre H and radius HE.
6. With centre B and radius BF draw an arc.
7. With centre D and radius DE draw an arc.

1. You have now drawn the 4 arcs to complete the construction.

Figure 27 - 4-Arcs Method of Constructing an Isometric Ellipse

Figure 28 shows similar methods for isometric 4-arcs in different isometric positions.

Figure 28 - 4-Arcs Method used in Other Isometric Positions

Note: This method does not produce accurate isometric circles (ellipses), but is sufficiently accurate for the construction of isometric ellipses up to about 50 mm in diameter. For larger isometric ellipses, it is advisable to use the more correct method, involving the plotting of points along the ellipse curve and then drawing a fair curve through the points so obtained. If the 4-arcs method is used with larger ellipses, the resulting drawing will have a distorted appearance.

Figure 29 is an example of an isometric drawing, which involved the construction of ellipses on three faces using the 4-arcs method of construction.

 

Figure 29 - Example of an Isometric Drawing Involving Isometric Ellipses on Three Faces using the 4-Arcs Method of Construction

Drawing Isometric Curves

The method of drawing ellipses (from circles) in isometric drawings as shown in Figure 16 is suitable for the drawing of more complicated shapes and curves in isometric drawings as shown in Figure 30. This illustration shows:

1. A Front view of the object to be drawn with vertical lines along its outline - these lines are often referred to as ordinates.
2. The vertical lines have been transferred to the isometric drawing with the same spacings between the verticals along the 30 degree axis.
3. The lengths of the lines have been transferred from the Front view onto the isometric drawing.
4. 30 degree lines of the length of the thickness of the shaped object have been drawn from the upper ends of each ordinate in the isometric View.
5. A fair curve has been drawn through the points so obtained.

Figure 30 - Example of Drawing an Isometric Curve using the Ordinate Method of Construction

Estimated One and Two-Point Perspective Drawing

If you look carefully at any object, lines along its sides appear as if they are inclined to vanish towards what is known as a Vanishing Point or V.P. This illusion can be readily seen by looking along a pair of straight railway lines. The idea of V.Ps is the basis of the two geometrical methods - one-point (or single-point) and two-point perspective drawing.
Note: True perspective drawing involves a third V.P., but 3-point perspective drawing is beyond the scope of a book of this nature. However it must be remembered that one-point and two-point perspective drawing do not give true perspective and so may at times appear inaccurate. The two methods do, however, provide an excellent and easy method of drawing very well suited to the preparation of drawings for designs.

Estimated One-Point Perspective Drawing

Figure 31 is an example of a one-point perspective of a stepped platform. Note the following:

1. The position of the single V.P. can be in any position above, to the right, to the left or below a Front view of the object being drawn. If the V.P. is below, then a view from below the object will be drawn.
2. From the Front view draw lines to the V.P.
3. Complete the rear of the object with lines between the lines to the V.P. Lengths along the lines are estimated.

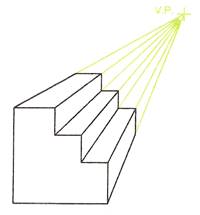
Figure 31 - Example of a One-Point Perspective Drawing

 

 

A second example is given in Figure 32, involving a semi-circular part. In this example a line from the centre of the semi-circle has been drawn to the V.P. in order to find the centre of the arc at the rear of the object.

Figure 32 - One-Point Perspective Drawing that Includes an Arc