Mechanical Behavior materials

For a structural material we ask the questions: “How strong it is?”  “How much deformation will it undergo?”  The answers to these questions determine the mechanical behavior of a material.  Simply put, mechanical behavior describes a material’s response to a load.
Metals are most commonly associated with structural applications; however ceramics and engineering polymers are also used in structural applications. 
To get a handle on a material’s behavior (mechanical or otherwise), material properties are defined by professional organizations such as ASTM, ANSI, ASM, etc. The properties are defined according to carefully designed standard lab tests that attempt to replicate as nearly as possible the service conditions a material will encounter.  These material properties may depend on temperature, moisture, uv radiation, or other factors, even atmospheric oxygen or hydrogen.
Structural engineers determine the stresses and stress distributions that will develop in a material for different loading conditions.  It is the job of the material’s engineer to figure out how to produce and fabricate materials that will withstand these stresses.
Stress and Strain

• (engineering or nominal) (normal: F^ A ® C or T) stress, s = F
                                                                                                           Ao
• (engineering or nominal) (normal: C or T) strain, e = Dl
  lo
• elastic deformation (macroscopic and atomic level) – stretching of atomic bonds
• plastic deformation (macroscopic and atomic level) – distortion, breaking and reformation of atomic bonds
• true stress, s = F/Ai
• true strain, e = ln   (e= )      Note: If volume is constant Ai li = Ao lo Þ Þ e
• shear stress, t = F/Ao   where F // A
• shear strain, g  = tan q
• Hooke’s law shows a linear relationship between stress and strain:
  s = Ee   for normal stress     and    t = Gg   for shear stress
  For metals Hooke’s law applies to the elastic region where there are relatively low values of stress and strain. 
• Young’s modulus, E (aka elastic modulus or modulus of elasticity)
  This measures the resistance to the separation of adjacent atoms, i.e. interatomic bonding forces.  It is proportional to the slope to the atomic bonding force vs. atomic separation distance plot at the equilibrium point. 
• tensile modulus – usually refers to Young’s modulus for stress-strain curves of constant slope.
• elastic modulus – slope at beginning of curve if slope of stress-strain curve is not constant.
• tangent modulus – slope of line tangent to curve at point of interest if slope of stress-strain curve is not constant.
• secant modulus  – slope of line drawn from origin of curve to point of interest if slope of stress-strain curve is not constant.
• stiffness  =  E Ao
  lo
• shear modulus, G (aka modulus of rigidity)
• Poisson’s ratio, n – the ratio of lateral strain to longitudinal strain =  - ey/ex = - ez/ex
  The ideal ratio (for no volume change) = 0.5  The average value for materials is approximately 0.3
• Isotropic materials have the same Poisson’s ratio for all lateral directions.
• for isotropic materials and small values of strain, E, G and n are related by:   E = 2G (1 + n)
• 
• the standard tensile test
• linear region
  proportional limit
• elastic region
• yielding
  yield point phenomenon
• plastic region
• elastic strain recovery
• set
• strain hardening region
• necking
• The plot of true stress vs. true strain in the strain hardening region can be approximated by:
  sT = K eT n 
  where K and n are constants for a given metal depending on its thermomechanical history 
  Note:  this is a line in on log-log plot with a slope of n
• yield strength, Sy or Y.S. 
  offset yield point
• ultimate strength, (aka tensile strength), Su or T.S. 
  Note the difference between the words strength & stress.
• specific strength – the word specific generally refers to a property per mass (or weight) of the material.  In this case it refers to the strength per unit density of a material.
• residual stress – stresses that remain in the material after the applied stress is removed.
• ductility (reduction of area and elongation)
• brittle behavior
• toughness is the amount of energy that a material will absorb per unit volume before it breaks. 
  It is the area under the stress strain curve.  toughness
• fracture toughness, K1c – related to toughness, a material property from Fracture Mechanics.  Whereas toughness is a measure of ductility on a macroscopic scale, fracture toughness can be thought of as a measure of ductility on a microscopic scale.
• resilience – the elastic strain energy that a material absorbs per unit volume.
• 
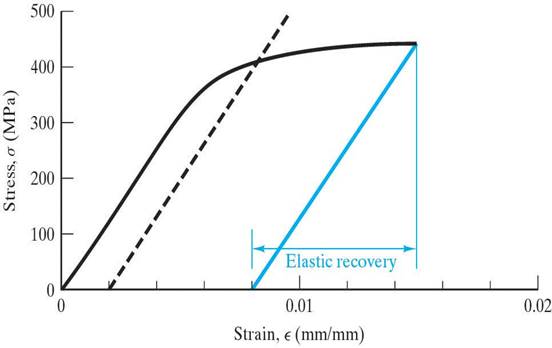
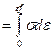
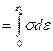• modulus of resilience, Ur   The area under the linear portion of the s-e curve.
• true stress at failure, sF
• true strain at failure, eF
• Ceramics are more brittle than metals.  Typically their TS <<<<< CS.  The Griffith crack model explains why:  All materials have elliptical cracks that experience a stress intensification at the crack tip given by:  sm = 2s (c/r)1/2   Ceramics and glasses have a lot of these.  A compressive load tends to close, not open the Griffith flaws.  Hence, the CS is not affected, only the TS.
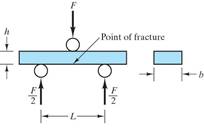• For ceramics and other brittle materials a more convenient property than the T.S. is obtained by a 3 point bending test that gives the modulus of rupture (MOR) or flexural strength (F.S.): MOR = 3FL
  2bh2
  
• For polymers the flexural modulus or modulus of elasticity in bending is more convenient than the Young’s modulus.  For the 3 point bending test   Eflex   =    L3m     where m is initial slope of load-deflection curve.                                                                            4bh3                                     
  This is a informative property because it describes the combined effect of T and C. (It is not so important for metals to describe a combined effect because they behave the same in T or C)
• For materials used for energy absorption such as elastomers, a modulus which characterizes the performance of the polymer under an oscillating load is the dynamic modulus of elasticity, Edyn = CIf2  where C is a geometry dependent constant, I is the moment of inertia of the beam and weights used in the test, and f is frequency of vibration.

Hardness (Mohs, Rockwell, Brinell, Knoop, Vickers, Durometer, Barcol)
A simple alternative to tensile test.  The test measures resistance to indentation by pressing an indenter into the material with a specific load and calculating a hardness number.  The hardness number is based on a formula using indentation geometry measurements.   It is a NDE (non-destructive examination).  Sometimes the hardness number can be correlated to the T.S. of the material.
Dislocations, Deformation Mechanisms,
The theoretical critical shear stress (i.e. the stress necessary to slide atomic planes over each other) for a material is roughly one order of magnitude less than the bulk shear modulus, G.  The actual stress necessary to plastically deform most materials is an order of magnitude less than this value. 

In other words, the theoretical strengths of perfect crystals are much greater than the experimentally measured values.

Why?  Because there are dislocations in the material!  (All crystalline materials have dislocations.
They come from the solidification process, plastic deformation, and thermal stresses during cooling.)

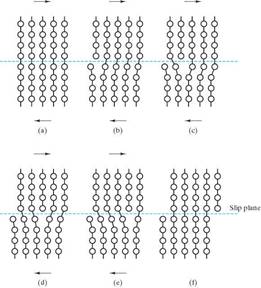
Dislocations facilitate the action of a step-by-step mechanism of deformation called slip.  The dislocation moves through the material, requiring only a relatively small shearing force in the immediate vicinity of the dislocation in order to produce a step-by-step shear that eventually yields the same overall deformation as the high-stress mechanism.  These discrete steps require much less energy than if all the atomic bonds in the slip plane needed to be broken at once.

 

Slip is more difficult as the individual atomic step distances are increased.  Hence, slip is more difficult on a low-atomic-density plane than on a high-atomic-density plane.

 In general, the micromechanical mechanism of slip – dislocation motion – will occur in high-atomic-density planes and in high-atomic-density directions. 

A combination of families of crystallographic planes and directions corresponding to dislocation motion is referred to as a slip system. 

For example the fcc slip system is  {111} <110>.
This is 12 “systems”.
The hcp slip system has only has 3 systems.
Hence, fcc materials are more ductile than hcp materials.

Consider the deformation of a single crystal material

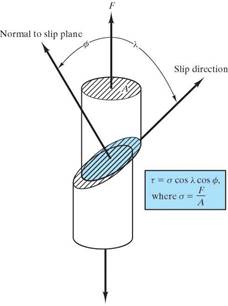
resolved shear stress, tr
is the actual stress operating on the slip system
resulting from the application of a simple tensile stress:
           slip plane

Schmid’s Law:
where
s is the applied tensile stress
f is the angle between the applied stress and the normal to the slip plane
l is the angel between the applied stress and the slip direction.

critical resolved shear stress, tc
is the value of the resolved shear stress that produces dislocation motion. 
This is a material property that is approximately equal to the yield strength.

When tr = tc then we have slip. 

 

Consider the deformation of a poly-crystalline material
In a polycrystalline material, the direction of slip varies from one grain to another.  For each grain, dislocation motion occurs along the slip system that has the most favorable orientation to the applied stress.  Mechanical integrity and coherency are maintained along the grain boundaries; hence, each grain is constrained by its neighbors.  Grains become elongated in the direction of the applied stress. 

Poly-crystalline materials are generally stronger than single crystal materials for 2 reasons:

1. Even though a single grain may be favorably oriented with the applied stress for slip to occur, it can’t deform until adjacent and less favorable oriented grains do.
2. Grain boundaries act as obstacles to slip.

 

Alternative deformation process to slip – twinning
If slip is restricted, another type of deformation mechanism may take place called twinning.  It is not as common as slip.  It can occur in bcc and hcp materials at low temperatures or high load rates. 

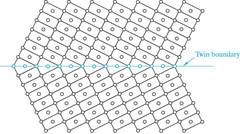
In twinning, shear forces produce atomic displacements such that after the displacements, atoms are located in mirror image positions on the other side of the twin plane.  Recall – this was the twin (grain) boundary. The displacements of the atoms are proportional to the distance from the twin plane. 

Like slip, twinning occurs in specific crystallographic planes and in specific crystallographic directions.  (e.g. in  bcc the twinning system is  {112}<111> )

Strengthening Mechanisms
Anything that acts to restrict or hinder slip (dislocation motion) renders a material harder and stronger.
The price is usually ductility.

 

What can act as “obstacles to slip”?

• grain boundaries (at low temperatures)
• impurity atoms (and the strain fields around them)
• dislocations

 

So three common strengthening mechanisms are:

1.  Grain Refinement
Finer grained materials have more grain boundaries per unit volume.  Grain size can be regulated by the rate of solidification or by plastic deformation followed by an appropriate heat treatment. 

Faster cooling during solidification will result in a finer grain structure.

A plastically deformed crystal lattice has high energy.  This high energy lattice provides more nucleation sites during recrystallization.  Hence more grains start to grow which results in a fine grained structure after recrystallization.

 2.  Solid solution strengthening (solution hardening)
Impurity atoms are added in such a way as to maximize their effectiveness to act as an obstacle to slip.

3.  Cold working (strain hardening or work hardening)
Plastic deformation will increase the dislocation density, change the grain shape and increase the strain energy of the crystal lattice. 

 

Creep
is the plastic deformation of a material at high temperatures (@0.4Tm) over long periods of time.

¨ The four variables of strain, time, temperature, and stress level make creep difficult to quantify.

¨ Typical experimental data gives “creep curves” for a constant temp and stress level:

¨ The steady state creep rate,  is the slope of the secondary stage and characterizes creep behavior.  Creep has a diffusional mechanism.  Hence it is a thermally activated process. 
So it should not be surprising that the steady-state creep rate has an Arrhenius form:
  where Q is the activation energy for the creep mechanism.

¨ Creep curves have increased strain for increased T or applied stress.

 

 

 

 

¨ A second importantant characterization of creep is the creep rupture tests that measure the time to rupture (rupture lifetime), tr, for particular values of temperature.


Sometimes these curves give the time to
0.2% strain instead of the time to rupture.

¨ Since ceramics are used in high-temperature applications, it is important to consider their creep characteristics.  Diffusion is more complicated in ceramics and so the dominant mechanism of creep is the sliding of adjacent grains along their grain boundaries. Some impure refractory ceramics have a glassy phase at the grain boundaries, and so the mechanism of sliding there is due to viscous deformation of this glass phase.  In either case, the easy sliding mechanism at the grain boundaries is generally undesirable due to the resulting weakness at high temperatures. Hence coarse grain materials are preferred for applications at high temperatures.

¨ Creep can be operative at low temps if the material has relatively low melting points.  Hence creep can occur in poymers at room temperature.

¨ Stainless steels and refractory metals are especially good for creep resistance.

¨ Factors that give materials good creep resistance:

• high melting temperature
• high elastic modulus
• less grain boundaries

 

Stress Relaxation
is a related phenomenon to creep and important for polymers.  It is the “relaxation” of stress over a long period of time and a corresponding permanent strain. 

Whereas    creep    involves  increasing  strain over time for materials under constant stresses,
stress relaxation involves decreasing stress over time for materials under constant strains.

The mechanism of stress relaxation is viscous flow (i.e. molecules gradually sliding past each other over an extended period of time.)  Viscous flow converts the elastic strain into non-recoverable plastic deformation. 

The relationship between the stress and time is given by

• = so e –t/t 

where t is the relaxation time and characterizes the phenomenon of stress relaxation. 
t  is the time necessary for the stress to fall to 37% of the initial stress.

Since viscous flow is a thermally activated process it should not be surprising that the relaxation time has an Arrhenius form:

Glass Solidification Behavior & Glass Deformation Mechanisms
Crystalline materials deform by the motion of dislocations.
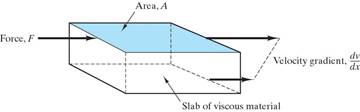
Noncrystalline materials deform by viscous flow, the same type of deformation found in liquids. 
With applied stress, groups of atoms slide past each other. 

Viscous flow is characterized by this equation:            
t =  h  dv/dy                       
where h is the material property of viscosity. 

As we can see from this equation, viscosity is the proportionality constant between the applied shear stress and the velocity gradient.   The units of viscosity are poises (P) or Pascal-seconds (Pa-sec):  1P = 0.1 Pa-sec    (Note: h is the reciprocal of the material property of fluidity.)

The behavior of glasses is compared with crystalline materials in this plot of specific volume

The supercooled liquid is the material just below Tm where it still behaves like a liquid – deforming by viscous flow mechanism.  It is in a rubbery, soft plastic state above Tg, the glass transition temperature.

The term supercooled liquid is often used synonymously with glass. Strictly speaking, however, the term supercooled liquid is the material between Tg & Tm and the term glass is the material below Tg, where it has become a truly rigid solid, (although still noncrystalline,) deforming by an elastic mechanism.  Below Tg it is in a rigid, brittle glassy state.

Note:  the slope of this curve is related to the thermal expansion coefficient.  The thermal expansion coefficient above Tg is comparable to that of a liquid. Below Tg it is comparable to a solid.

At a temperature above Tg the material will reach a point where it becomes so fluid that it can’t support the weight of a probe.  This is the softening temperature.

Viscoelastic Deformation of Glasses
The viscosity of a typical soda-lime-silica glass as a function of temperature is shown here.  As T increases, the viscosity decreases and viscous flow becomes easier.  At room temperature, the glass is elastic.  Above Tg it is viscous. Hence the deformation behavior of glasses is termed viscoelastic.

Various reference points of viscosity are defined that are useful in the processing and manufacture of glass products:

• 
• Melting point – The temperature where the material is fluid enough to be considered a liquid. This corresponds to a viscosity of about 100 P.  (The melting range is h between 50 and 500. Compare with water which has h = 0.01P)
• Working point – The temperature corresponding to 104 P.  At this temperature glass fabrication operations can be carried out.  (The working range is h between 104 and 108 P)
• Softening point – 107.6 poises.  At this temperature the glass will flow at an appreciable rate under its own weight. 
• Annealing point – 1013.4 poises.  Internal stresses can be relieved in about 15 minutes at this temperature. This is roughly Tg. (The annealing range is 1012.5 to 1013.5)
• Strain point – 1014.5 poises.  Below this temperature the glass is rigid and stress relaxation occurs only at a slow rate.  In other words, there is little plastic deformation before failure.  The interval between the annealing and strain points is commonly considered the annealing range of a glass.

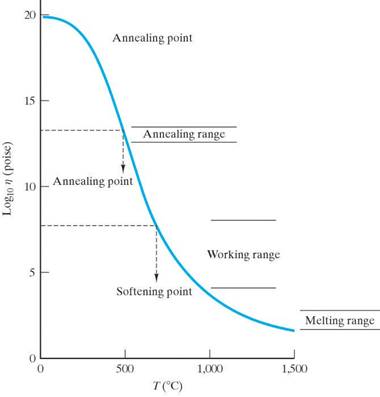
A hard glass has a high softening point
A soft glass has a low softening point.
A long glass has a large temperature difference between its softening and strain points.

Above Tg, viscosity follows an Arrhenius form:  h = ho e +Q/RT               where Q is the molar activation energy for viscous flow. (The sign on  the exponent would be negative if we considered fluidity instead of h)

Thermal Shock is fracture due to rapid cooling.  Fracture occurs because thermal stresses are induced due to temperature gradients which create different expansions.  Glasses are particularly vulnerable to thermal shock because of their brittleness.  To avoid thermal shock, anneal in the annealing point temperature range.  

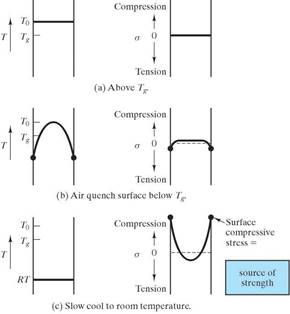
To make glass stronger, we introduce residual compressive stresses in the surface.
The breaking strength of the glass will then be the sum of the tensile strength of the glass plus the residual compressive stresses introduced into the surface.  The two methods to do this are heat treating (to get tempered glass) and chemically treating (to get chemically strengthened glass.)
Tempered glass:                                      
Consider the process for producing tempered glass:

Bring glass to equilibrium above Tg

 

• Surface quench it to form a rigid surface “skin” that is below Tg while the interior is still above Tg
  
  - this results in interior compressive stresses that are largely relaxed, and a modest tensile stress present in the skin.
  
• A slow cool to room temperature allows the interior to contract considerably more than the surface causing a net compressive residual stress on the surface balanced by a smaller tensile residual stress in the interior. 

 

Chemically strengthened glass:
The process of chemically treating glass is to chemically exchange the larger radius K+ ions for the Na+ ions in the surface of a sodium-containing silicate glass.  The larger ions produce compressive stresses in the surface.

Deformation of Polymers
Polymers in general experience large elastic and plastic deformations. (Hence the term “plastics”.)

 

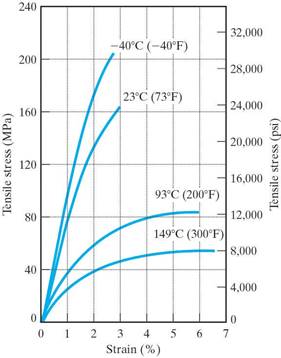
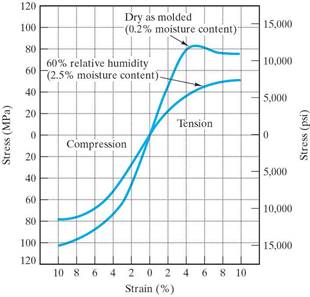
More than other materials, the properties of a polymer may vary with moisture content of the environmnent, uv radiation, or other factors.
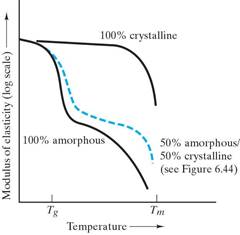
Consider the plot of modulus of elasticity as a function of temperature for a typical thermoplastic with approximately 50% crystallinity:

Below Tg the polymer behaves like a metal or ceramic. (Although the value of the modulus is substantially lower.) 

In the Tg range, the modulus drops precipitously and the mechanical behavior is termed leathery – it can be extensively deformed and slowly returns to original shape upon removal of the stress.

Just above Tg a rubbery plateau is observed.  In this region extensive deformation is possible with rapid spring back to the original shape upon removal of the stress.

Notice that with polymers we have extensive nonlinear elastic deformation. 

When Tm is reached, the modulus again drops precipitously and we enter the liquid-like viscous region.  (A more precise term would be decomposition point rather than a melting point.)

 

The behavior of the 50% crystalline thermoplastic is midway between the fully crystalline material and a fully amorphous material.

A structural feature that will affect the mechanical behavior in polymers is cross-linking of adjacent linear molecules to produce a more rigid, network structure.  The effect is similar to increasing crystallinity.

 

Elastomers
are materials that experience vast elastic deformations.  The huge elastic strains in these materials are primarily due to uncoiling of the long chained molecules.  Deformation is also due to the sliding of molecular chains over each other (breaking and reforming secondary bonds) and then finally the stretching of primary bonds along the backbone of the carbon chain.  Hence the elastic modulus increases with increasing strain as shown here in the stress – strain curve for a typical elastomer:

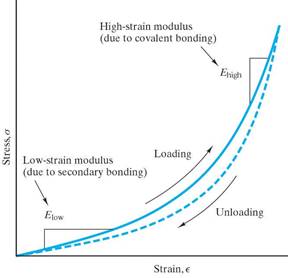
The low strain modulus has a low value because the forces needed to uncoil the molecular chains are small.  The high-strain modulus has a higher value because stronger forces are needed to stretch the primary (covalent) bonds.  Both regions involve overcoming secondary bonding, which is why the elastic modulus for these materials is significantly less than for metals or ceramics. 

Tabulated values for the elastic modulus for elastomers are usually for the low strain regions.

 

 

Note that the recoiling of the molecules (during unloading) has a slightly different path than the uncoiling (during loading).  This defines hysteresis. Hysteresis is behavior in which a material property plot follows a closed loop.  In other words, it does not retrace itself upon the reversal of an independent variable, in this case the stress.  The area of the loop is proportional to the energy absorbed in each cycle of the loading.

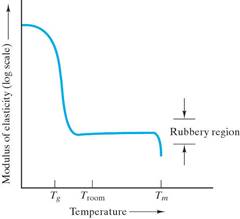
Consider the plot of modulus of elasticity as a function of temperature for a typical elastomer:  The rubbery plateau is pronounced and establishes the normal room-temperature behavior. (Tg  is below room temp.)

 

 

The plot of modulus of elasticity as a function
of temperature for some commercial elastomers:

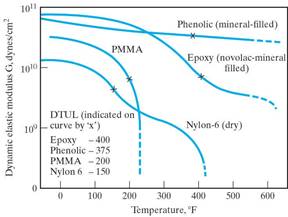
Note:  DTUL in these curves is the deflection temperature under load, a parameter frequently associated with Tg . (It is defined as the temperature at which a standard test bar deflects a specified distance under a load.  It is used to determine short-term heat resistance.  It distinguishes between materials that are able to sustain light loads at high temperatures and those that lose their rigidity over a narrow temperature range.)