Introduction:
In determining the fabrication and possible practical applications, the mechanical properties of materials, their strength, rigidity and ductility are of vital importance. The important mechanical properties of materials are: elasticity, plasticity, strength, ductility, hardness, brittleness, toughness, stiffness, resilience, malleability, fatigue, creep, etc. Materials exhibit a wide range of mechanical properties ranging, e.g., from the ductility of pure copper to the hardness of diamond and most surprising elastic behaviour of rubber. There are several materials behave quite differently when stressed in different ways, e.g. steel and wood are stronger in tension whereas cast iron, cement and bricks are much stronger in compression. Obviously, stresses can produce a shape change and may also cause a material to break or fracture. For materials which have to withstand high temperatures, the melting point is also of importance.
The combination of high yield strength and good fracture toughness or ductility makes steel an excellent structural material. Modern high strength low alloy (HSLA) steels have a very fine grain size around 10 micro-meters which provides both high strength and good crack growth resistance or fracture toughness.
In addition to mechanical properties of materials, the following properties are also important for an engineer, to enable him in selecting suitable metals for various jobs:
1- Physical Properties: These properties of materials include shape, size, colour, lusters, specific gravity, porosity, structure, finish, etc.
2- Technological Properties: We may note that all the technical properties of a metal are essentially its mechanical properties, which include properties like malleability, machinability, weldability, formability or workability, castability, etc.
3- Thermal Properties: Specific heat, thermal conductivity, thermal expansion, latent heat, thermal stresses, thermal shock, etc. fall under thermal properties of materials.
4- Electrical Properties: These include conductivity, resistivity, relative capacity, dielectric strength, etc.
5- Chemical Properties: These properties include atomic weight, equivalent weight molecular weight, atomic number, acidity, alkalinity, chemical composition, corrosion, etc.
Common Terms:
(i) Isotropy: A body is said to be isotropic if its physical properties are not dependent upon the direction in the body along which they are measured.
(ii) Anisotropy: The quality of variation of a physical property with the direction in a body along which the property is measured.
(iii) Elasticity: It is the property of a material which enables it to regain its original shape and size after deformation within the elastic limit. However, in nature no material is perfectly elastic, i.e., a certain limit exists for every material beyond which it will not be able to regain its original shape and size. This limit is termed as elastic limit. Materials with high elastic limit are called as more elastic than the others. This property is always desirable in metals used in machine tools and other structural constituents. Steel and rubber are amongst the common examples of materials having elasticity.
(iv) Plasticity: It is the ability of material to be permanently deformed (without fracture) even after the load is removed. It is of importance in deciding manufacturing processes like forming, shaping, extruding operations etc. Metals possess more plasticity at high temperatures. Usually, plasticity of a material increases with increase in temperature.
(v) Ductility: It is defined as the property of a metal by virtue of which it can be drawn into wires or elongated before rupture takes place. It is measured by the percentage of elongation and the percentage of reduction in area before rupture of test piece.

Similarly, the term percentage reduction of cross-sectional area is the maximum decrease in cross sectional area.

Ductility is a measure of the amount of permanent deformation that has occurred when the material reaches its breaking point.
Metals with more than 15% elongation are considered as ductile. Metals with 5 to 15% elongation are considered of intermediate ductility. However, the metals with less than 5% elongation are considered as brittle ones.
(vi) Strength: It may be defined as the capacity of material by virtue of which it can withstands or support an external force or load with rupture. It is expressed as force per unit area of cross-section. This is most important property of a metal, which plays a decisive role in designing various structures and components.
A material has to withstand different types of load, e.g. tensile, compressive and shear load. Accordingly, one may broadly classify strength into :
1-Depending upon the value of stress, the strengths may be elastic or plastic.
2-Depending upon the nature of stress, the strengths of a metal may be tensile, compressive, shear, bending and torsional. Now, we study all these types of strengths.
Ultimate strength: It is the load required to fracture a unit cross-section of material.
Elastic Strength: It is the value of strength corresponding to transition from elastic to plastic range, i.e. when material changes its behaviour from elastic range to plastic range.
Plastic strength: It is the value of strength of the material which corresponds to plastic range and rupture. It is also termed as ultimate strength.
In actual practice, a specimen is subjected to a stress which is always less than the working stress. The ratio of ultimate stress to the working stress of a metal is termed as factor of safetyor factor of ignorance. This greatly depends upon the nature of loads or stresses.
Tensile Strength: It is the maximum tensile stress which a material is capable of developing when subjected to loading up to rupture. Mathematically,

The tensile stress is expressed in N/mm2 or MN/m2.
Tensile strength is obtained from the following relation:

It is measured by the highest point on the conventional stress-strain curve. This strength provides the basic design information on the material’s acceptance in engineering tests.
(vii) Stress and Strain: Stress is defined as the force per unit area and strain as the fractional change in length, area or volume.


The stress is said to be normalif load P is normal to the surface and tangentialor shearing, if load is tangential to this surface. The normal or direct (tensile or compressive) stress is produced over a section when force is acting normal to the section. If the force is acting away from the section, the stress is tensile, if it is acting towards the section the section is compressive.
Strainis the deformation produced per unit length of a body due to the effect of stress on it. It is the ratio of the change in length of the specimen to its original length. If L is the original length of the sample and l is the change in length, then longitudinal strain,

Strain is simply a ratio and has no unit and it is a dimensionless quantity. Depending upon the type of load, strain can be lateral strain or shear strain.
As there are different types of stresses, there are different types of strains, e.g. (i) tensile strain (ii) compressive strain, (iii) shear or transverse strain and (iv) volumetric strain.
The strain associated with the change in length is called the elongation strain (l/L). Similarly ∆V/V is the volume strain where V is the volume. When there is a change in shape and no change in volume, corresponding strain is called shear strain. The shear strain is measured by the angle. The behaviour of a material within the elastic limit is the same under compression as under tension.
Corresponding to elastic and plastic properties of materials, we have two classes of strain:
(b) Plastic Strain: This is the permanent change in the body when subjected to a load. The change remains even after the applied load is removed.
The amount of elongation, expressed as a percentage of the original gauge length is called as the percentage elongation:
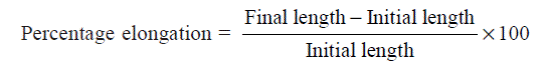
(viii) Hooke’s Law: In 1678, Robert Hooke, for the first time stated that within elastic limits, stress is proportional to strain, i.e.
![]()
The ratio of stress to strain is a constant characteristic of a material, and this proportionality constant is called modulus of the material. It differs from material to material and for different nature of stresses. When the stress applied is tensile or compressive, the constant is called Young’s modulus of elasticity. The slope of stress-strain diagram up to the limit of proportionality is called Young’s Modulus of elasticity (Y or E)

When the shear stress (τ) and strain (γ) are used, it is called modulus of rigidity (G). It is given by :
![]()
G is also called shear modulus. G and E are related as :

Where υ is Poisson’s ratio.
For volumetric stresses and strains, the constant is called bulk modulus (K). The relation between K and E is :

Poisson’s ratio (υ):
When a specimen is stressed by a uniaxial force, it is strained in the direction of the force and also in a direction perpendicular to the direction of the force. The strain in the direction of force is called longitudinal strain and that perpendicular to it as lateral strain. The relationship existing between the lateral strain and axial strain is called Poisson’s ratio (υ):

Poisson’s ratio is an important elastic constant and its value is different for different materials. For most engineering structural materials its value is usually between 0.3 and 0.6. The relation between E, G and υ is :

Source: http://www.uobabylon.edu.iq/eprints/pubdoc_2_19402_348.doc
Web site to visit: http://www.uobabylon.edu.iq/
Author of the text: indicated on the source document of the above text
Stress :
Resistive force per unit area is called stress. Its units are N/mm2. it is the representation of atomic forces developed as such external forces changes the equilibrium position of atoms (bond length). The nature may be Compressive or tensile, depending upon the nature of externally applied load.
Strain :
The change in length per unit initial length is called strain. It is the change in length of intermolecular distances over the bond length. The nature may be Compressive or tensile, depending upon the nature of externally applied load.
Young’s Modulus :
Within elastic limit loading, the deformation of the material is about 0.1% to 0.2%. in this range (within elastic limit), the stress is directly proportional to strain. It is known as Hooke’s Law. To make them equal, a proportionality constant appears, which is termed as Modulus of Elasticity or Young’s Modulus.
Modulus of Elasticity or Young’s Modulus = Stress / Strain
Young’s modulus is strongly influenced by :
Poisson Ratio :
When a material is subjected to tensile stress, it get elongated along its length while its cross section get reduced. The length wise strain is termed as Longitudinal Strain and strain in other two axes are termed as Transverse Strains. Say, loading is in x direction, then the strain in x-direction is called Longitudinal Strain, and strains in Y-axis and Z-axis directions are termed as Transverse Strains. The ratio of Transverse Strain to Longitudinal strain is called Poisson’s Ratio. Its value varies from 0 to 0.5.
Shear Modulus :
The ratio of shear stress to shear strain is called shear modulus. It is also known as Modulus of Rigidity (G). Its relation with Young’s Modulus and Poisson’s Ratio is as G = E / [ 2 (1+n) ]
Bulk Modulus :
A material under three-dimensional loading is subjected to the stresses assX, sY, sZ, along x, y, Z axis respectively. Thus, the change in volume becomes as dV. The bulk modulus or modulus of elasticity of volume K is defined as the ratio of Average Stress savg to the volumetric strain.
K = Average Stress / Volumetric Strain
Average Stress = (sX + sY + sZ ) / 3
Volumetric Strain = dV / V = ex + eY + eZ
K = E / 3 [ 1- 2n]
Isotropy :
The material in which all the planes are plane of symmetry and the properties all the directions possesses the same value, are known as Isotropic Materials. Number of independent elastic constants are only two. Isotropic materials obeys the Hooke’s Law. All the metals are assumed as Isotropic.
Anisotropy :
In an anisotropy materials, there is no plane of symmetry and thus, e properties are direction dependent. The number of elastic constants in most general case is 36, out of which 21 are independent. Anisotropic materials such as Composites obeys Generalized Hooke’s Law (different from Hooke’s Law).
Orthotropy :
Orthotropic Materials are those materials in which number of elastic constants are 12 out of which 9 are independent. In such materials, properties are having same value in some directions while possesses different values in some directions. Example is Unidirectional Fiber Composite.
Homogeneity :
When the materials properties do not change from one point to another point in a certain direction, then the nature is called Homogeneity.
Heterogeneity :
When the properties are changed from one point to another point along any direction, then the nature of materials is called Heterogeneity.
Stress Strain Diagrams : Discussed in the Class
Bi-Modulus Materials :
The materials, whose stress-strain diagram has different slope in tension and compression (even till the elastic limit), are known as Bi-modulus Materials. They possess unequal values of Young’s Modulus in tension and compression. Cast Iron is not the bi-modular material while wood and elastomers are bi-modulus materials.
Damping Property :
The loading and unloading curve for any material is known as Mechanical Hysteresis Loop. In such cases, loading curve and unloading curve are not the same. The strain energy stored in the material due to loading is not always recoverable. Such loss of strain energy is in the form of internal friction. Such loss of energy is termed as damping loss and analogous property is termed as Damping property. Example : Rubber.
Strength :
The ability of a material to withstand with the loading without failure is known as strength. There are various types of strengths, depending upon the type and nature of loading as : Tensile Strength, Compressive Strength, Torsional Strength, Shear Strength etc. The strengths are of following types :
Elastic Strength :
The highest stress value till that he behaviour of the material remains elastic. It is generally measured at the end of proportional limit.
Ultimate Strength :
It is the value of maximum stress sustained by the material without failure. It the stress value corresponding to the highest point or peak value of stress in the stress-strain curve.
Breaking Stress :
The highest stress which is attained by the material at the time of failure is known as breaking stress or breaking strength.
Specific Strength :
Specific strength is the strength per unit density of the material. It can be elastic specific strength (corresponding to elastic strength) and ultimate specific strength (corresponding to ultimate strength). A material with high specific strength is required in light weight constructions. Composite materials possess more specific strength with respect to conventional materials and hence used widely in aircrafts, satellite and space-going vehicles.
Stiffness :
The ability of material to resist the elastic deformation or deflection is known as stiffness. It depends upon the shape of the material in structure and machine component. Mathematically, load per unit deflection is known as stiffness.
Elasticity :
Ability of the material to regain its original shape and size after the removal of external loading is termed as elasticity. In this case, the deformations are completely recoverable.
Plasticity :
The ability of the material to undergo permanent deformation or non-recoverable deformations, is known as plasticity. The materials do not obey Hooke’s law in plastic region. The relation of stress-strain is as : s = E en where power index n is not equal to unity. When n = 1, region is elastic.
Resilience :
The stored energy wit in the material is termed as strain energy. It works when external loading is being removed to recover the deformation, if so. Resilience or strain energy is the capacity of the material to absorb the energy with in elastic limit. Proof Resilience is the amount of maximum energy stored upto elastic limit.
Toughness :
Toughness is the strain energy absorbing capacity of a material in both elastic and plastic deformation upto fracture.
Hardness :
Ability of the material to resist indentation, abrasion and scratching is known as hardness. It is related to elastic limit deformation and their resistance. Hardness is corresponding to proof resilience.
Ductility :
The ability of the material to deform permanently is known as ductility. It is associated with the tensile loading. Total elongation includes elastic and plastic deformations (recoverable and non-recoverable). Ductility is the ability of the material to be drawn into the form of wires.
Brittleness :
The ability of the material to resist the plastic deformation (elongation) beyond elastic limit is known as Brittleness. Those materials, which fail with negligible permanent elongation, are known as Brittle Materials. The strains are 5% maximum in Brittle Materials.
Malleability :
The ability of material to deform permanently is also known as malleability. In this case, nature of loading is compressive. The ability of the material to be pressed into the form of sheets (under compressive load) is known as Malleability. It permits large plastic deformation under the influence of compressive loads.
True Stress :
Conventional stress are those stress in which original cross sectional area is taken for calculation of stress value even at yielding or permanent deformation range. As volume of the material remains constant, thus, when length increases (say – under tensile loading), cross-sectional area will reduce. Thus, in plastic range, the conventional stress value will be different from the value that is obtained by taking actual cross-sectional area at that point. This stress is known as True Stress. Thus, True Stress is the resistive force per unit actual area (at that point). Mathematically, sT = sC (1 +eC)
True Strain :
The change in length per unit intermediate preceding length (in place of original length – taken once only) is known as true strain. Mathematically, eT = ln (1 + eC )
Fatigue :
It is being observed that when repetitive, cyclic loading and unloading for large number of cycles is there on any material, then the failure occurs prior to the elastic limit. The behaviour of the material under such loading is known as fatigue. Such type of early failure is known as Fatigue Failure. The limit at which failure occurs is known as Endurance Limit or Fatigue Strength. In such failure, rate of loading is not the factor responsible for failure. Fatigue limit is about 0.3 to 0.5 times that of ultimate strength of the material.
The main effects of fatigue on the properties of the material are as :
The mechanism of fatigue failure includes :
Improving Fatigue Life :
Creep :
The permanent deformation (strain) produced under the steady load after some time is known as creep. In such plastic deformation, load remains constant and the amount of deformation depends upon the time of load action. Thus, mechanical creep is the time dependent function. It is also influenced by the temperature. The various application areas of creep are as :
The time for the deformation is dependent upon the :
Creep Curve :
The creep curve is as follows :

The various stages are as :
Transient Creep or Cold Creep :
This range is non-linear and rate of deformation (creep) is more at initial stage but slows down at later stage. This part of creep occurs at very low temperatures or at room temperatures. It is also termed as Primary Creep or First Stage of the Creep.
Viscous or Hot Creep :
This range of deformation is somewhat linear. Such type of creep occurs at high temperatures and thus known as hot creep. It is also termed at Second stage of the creep or secondary creep.
Tertiary Creep :
It is the last stage of the deformation before the creep failure. Creep failure is the failure of the material due to creep phenomena. In this range, rate of straining is too fast to neck formation in the materials. It is also known as Third Stage of Creep.
Mechanism of Creep :
Occurrence of the creep in the material is supposed to be the effect of the following :
Creep Resistant Materials :
The parts, which are to be used at elevated temperature, must be creep resistant. The components, which are used even at high pressure, should also be of creep resistant materials. Some such materials are as :
Nickel using thoria by dispersion hardening method is the best creep resistant material. It can maintain its strength upto 0.9 TM. Some special materials are as :
Creep Laws :
Primary, secondary and tertiary stages of the creep follows different creep laws for various materials. The variation of creep strain (ecr) with time (t) may be expressed as :
Andrade’s Law (of Transient creep) :
It is for metals and some plastics. The creep strain and time are related as ecr = C tn , where C is the constant and n is index (value = 1/3).
Logarithmic Law (of transient creep) :
It is for glass and rubber. The creep strain and time are correlated as : ecr = K ln [ 1 + ( t/t1 ) ], where K is the constant and t1 is the arbitrarily chosen time.
Hyperbolic Law (of transient creep) :
It is for Concrete. The creep strain and time are correlated as : ecr = l t / ( n+t) , where l is the constant and n is the creep time constant.
Secondary Creep Law :
It is stated as : ecr = el + vcr t , where el is creep intercept and vcr is viscous or minimum creep rate. Minimum creep rate increases with increasing stress and is given by : vcr = A sn where A, n are the constants (n > 1).
==========================
Source: http://www.oocities.org/yantrikians/MSU2.doc
Web site to visit: http://www.oocities.org/
Author of the text: indicated on the source document of the above text
If you are the author of the text above and you not agree to share your knowledge for teaching, research, scholarship (for fair use as indicated in the United States copyrigh low) please send us an e-mail and we will remove your text quickly. Fair use is a limitation and exception to the exclusive right granted by copyright law to the author of a creative work. In United States copyright law, fair use is a doctrine that permits limited use of copyrighted material without acquiring permission from the rights holders. Examples of fair use include commentary, search engines, criticism, news reporting, research, teaching, library archiving and scholarship. It provides for the legal, unlicensed citation or incorporation of copyrighted material in another author's work under a four-factor balancing test. (source: http://en.wikipedia.org/wiki/Fair_use)
The information of medicine and health contained in the site are of a general nature and purpose which is purely informative and for this reason may not replace in any case, the council of a doctor or a qualified entity legally to the profession.
The texts are the property of their respective authors and we thank them for giving us the opportunity to share for free to students, teachers and users of the Web their texts will used only for illustrative educational and scientific purposes only.
All the information in our site are given for nonprofit educational purposes