Simple harmonic oscillators show resonance if they are forced to vibrate at their natural frequency. This is a phenomenon of great importance in many aspects of science.
Summary
Discussion: Resonance as a phenomenon. (10 minutes)
Demonstration: Barton’s pendulums. (10 minutes)
Student activity: An applet of a forced pendulum. (20 minutes)
Student experiment: A selection of model systems. (30 minutes)
Student questions: Questions on resonance. (40 minutes)
Discussion: The effect of damping on resonance. (10 minutes)
Demonstration and student reading: The Tacoma Narrows bridge disaster. (30 minutes)

Discussion:
Resonance as a phenomenon
An oscillator can be forced to vibrate with increasing amplitude; to do this; energy must be supplied in the right way.
A child on a park swing is the classic example that all can visualize. The push must come at the same natural frequency as the oscillating pendulum-like swing and at the right point in the swing’s cycle.
So the energy input system must be ‘tuned’ to the oscillator, or the oscillator must be able to be tuned to the available energy input. Matching up the natural frequency and the forcing frequency results in a resonant system. The fundamental resonant frequency is synonymous with the natural frequency of an oscillator.
Resonance can lead to very large oscillation amplitudes that can result in damage. E.g. buildings etc need to have their natural frequency very different from the likely vibration frequencies due to earthquakes.
Demonstration:
Barton’s pendulums
Barton’s pendulums are a famous demonstration of a resonance effect.
TAP 307-1: Barton’s pendulums
Student activity:
An applet of a forced pendulum
Investigate a virtual pendulum which can be forced.
http://monet.physik.unibas.ch/~elmer/pendulum/index.html
TAP 307-2: Forced oscillations
Student experiment:
A selection of model systems
Students can be allocated to one of the following experiments (duplication is easy), followed by a brief plenary session where each system is demonstrated to the whole class.
TAP 307-3: Book on a string
TAP 307-4: Resonance of a milk bottle.
TAP 307-5: Resonance of a hacksaw blade.
TAP 307-6: Resonance of a mass on a spring
Student questions:
Questions on resonance
TAP 307-7: Oscillator energy and resonance
TAP 307-8: Resonance in car suspension systems
TAP 307-9: Car suspension
Discussion:
The effect of damping on resonance
If a resonant system is forced at frequencies above or below the resonant (natural) frequency f0, the amplitude of oscillation will be reduced. The ‘resonance curve’ peaks at f0. You may need to discuss how the shape of the curve depends on the degree of damping.
TAP 307-10: Resonance
Demonstration and student reading:
The Tacoma Narrows bridge disaster.
The Tacoma Narrows bridge disaster is generally described as a consequence of resonance. However, the full details of the mechanism are still debated. If possible show a video of the bridge as it collapsed in high winds on 7 November 1940. However, it seems more than likely that it is an example of positive feedback, a sort of “inverse damping” which created this effect.
TAP 307-11: Tacoma Narrows bridge
TAP 307-12: Tacoma Narrows: Re-evaluating the evidence:
TAP 307- 1: Barton’s pendulums
Apparatus
Set up:
Make one driver pendulum with a heavy bob and several light pendulums of various lengths with one length exactly matching the driver. Suspend all the pendulums from a string as below, and support the ends of the string firmly.
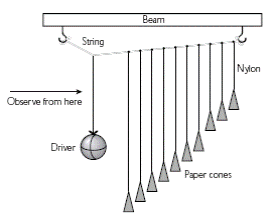
The demonstration is most effective in a darkened room with the cones brightly illuminated by a slide projector.
Students look along the line of the pendulums and observe what happens when the paper cones are at rest and then the driver pendulum is released from a widely displaced position.
The effective damping may be reduced by slipping plastic curtain rings over the cones and is easily done if the rings have a single cut in them.
Practical advice
This classic demonstration shows the effects of resonance (and non-resonance). Draw attention to the initial transient oscillations that die away. Bring out the point that the pendulums then all oscillate at the driving frequency, but the ‘resonant’ pendulum oscillates with the greatest amplitude.
As an extension, you can also illustrate how damping affects resonance. Weight each paper cone, (e.g. with a plastic or metal ring, such as a curtain ring), so that it is less affected by air resistance. The transient oscillations take longer to die away, and when the ‘steady state’ is reached the amplitude of the resonant pendulum is larger.
You may wish to bring out the following points:

The graph above shows two frequency response curves for an oscillator – in (a) there is very little damping but in (b) the oscillator is more heavily damped. The peak in (b) is broader, and it is the width of the peak that gives us a measure of damping.
Technicians note.
The wooden rod must be firmly clamped and be horizontal. It is very easy for the cones to tangle so the apparatus must be ready and set up in the classroom. (It is possible to manage without a wooden beam but it is easier to keep with one).
The lengths of the pendulums can be from a quarter to three quarters of a metre with the driver pendulum a half metre long. Nylon thread supporting the cones may be attached to the string by a half hitch or slip knot; this makes it easier to adjust lengths. The pendulums should be close together. Plasticine has been used successfully to secure the cones though a knot will suffice. If damping is to be shown plastic curtain rings that have 1 cut with a hacksaw so they can be slipped over the cones are good.
External references
This activity is taken from Salters Horners Advanced Physics, section BLD, activity 11 and additional sheet 9, with an adaptation of Revised Nuffield Advanced Physics experiment D15.
TAP 307- 2 Forced oscillations
Apparatus
What to do
This site contains an applet for a pendulum driven by a sinusoidally varying force:
http://monet.physik.unibas.ch/~elmer/pendulum/index.html
Set g= 9.8 N kg-1 and choose a suitable length l.
Predict the natural frequency of the pendulum using the equation you found earlier.
![]()
Set the driving frequency to be the same as your predicted natural frequency.
Set the amplitude of the driving force to 0.3.
Set the damping to zero.
Observe the resulting motion of the pendulum.
Use the ‘oscilloscope trace’ to plot a displacement–time graph for the pendulum.
Explore what happens if you alter the driving frequency.
Explore what happens if you increase the damping.
Practical advice
This ‘lab’ gives students further experience in using a spreadsheet to process (simulated) data using log-log graphs, and then goes on to illustrate the effect of the driving frequency and damping on forced oscillations. The first part could arguably be done easily and more authentically using a real pendulum, but the strength of the simulation is that it enables forced oscillations to be explored quantitatively with relative ease.
External reference
This activity is taken from Salters Horners Advanced Physics, section BLD, activity 18
TAP 307- 3: Book on a string
Swing!
High-amplitude oscillations will build up when the driving frequency applied to an oscillator matches the natural frequency of the oscillator. This is a very quick and simple demonstration that shows just that.
You will need
Blow by blow
![]()


The book can be made to swing quite dramatically by giving it short blows of air at the correct point of its motion. This is rather like pushing a child on a swing. Get the timing right and the book will move through a considerable angle.
What happens if you blow every second swing?
What happens if a friend blows from the other side in time with the swing?
You have seen
1. That the book will swing through large angles (will have a large amplitude) when the driving frequency matches its natural frequency.
Practical advice
This is a very simple but highly effective demonstration. It can be used for open days on a large scale, with strings hanging from the ceiling. It can be used as a vehicle for a qualitative discussion of damping and that steady amplitude is reached when:
energy in per cycle = energy out per cycle.
Social and human context
Another use for outdated textbooks!
External reference
This activity is taken from Advancing Physics chapter 10, 320E
TAP 307- 4: Resonance of a milk bottle
You will need
What to do
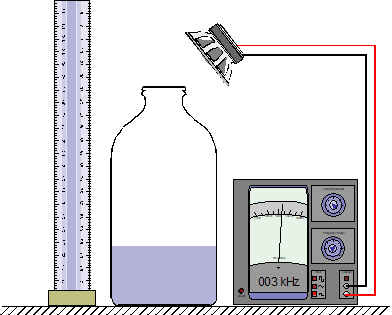
1. Take a milk bottle or beer bottle and fill it from the tap.
2. If you filled the bottle before reading this line, stop and start again! This time listen carefully to the sound you hear as the water fills the bottle. How would you describe the changes in pitch (or frequency) and loudness as the bottle fills?
3. Put a centimetre or two of water in the bottom of the bottle. Starting with a frequency of about 50 Hz gradually raise the pitch of the speaker whilst pointing the filter cone towards the open neck of the bottle. At a frequency in the range 100 to 400 Hz you will hear the amplitude of the sound rise markedly. At this point the air in the bottle is resonating.
4. Put a little more water into the bottle and find the resonance point again. Repeat this process until the bottle is full.
5. Plot your results (frequency at resonance / height of air in bottle) as you go.
6. Try to explain the observations you made when filling the bottle and listening to the sound in the light of the data.
You have seen
1. When the amount of air in a bottle decreases the resonant frequency goes up.
2. The splashing water must produce notes of many frequencies. The bottle selectively amplifies specific frequencies dependent on the depth of water.
Practical advice
This demonstration shows the resonant effects of a volume of air. Rather than just asking the students to listen to one resonance point, the initial puzzle brings out the frequency-matching nature of resonance. All sorts of frequencies are present in the splashing water, but the bottle selectively amplifies only specific frequencies – which is why the pitch of the note rises as the water level decreases.
250 ml or 500 ml beer bottles work nicely with this, but of course standard conical flasks or round-bottomed flasks can be used if preferred.
Alternative approaches
Students may suggest other resonating systems for exploration.
Social and human context
At a basic level the tuning by resonance is analogous to the tuning of electrical circuits in radios. There are electromagnetic waves of many frequencies all around, but the radio circuit tunes to a specific one through electrical resonance.
External reference
This activity is taken from Advancing Physics chapter 10, 330E
TAP 307- 5: Resonance of a hacksaw blade
When the driving frequency matches the natural frequency of an oscillator the amplitude of oscillation can rise dramatically. This is resonance. This experiment gets you to measure how the amplitude of an oscillating hacksaw blade changes with the frequency of the driver. The hacksaw blade is linked to the vibration generator by a piece of elastic cord. You will see the blade oscillate but will have to decide how to measure the amplitude of oscillation.
You will need
Optional:
Be Safe
|
Safety |
Setting up


What to do
Set the variable frequency generator at 1 Hz and measure the amplitude of oscillation. Repeat this at 1 Hz intervals up to 10 Hz. Keep a record of the results – but it is even more vital than usual to plot the results as you go, to see where extra readings are needed to define the curve.
Use the graph plotting package to produce a presentation-quality graph of your results. What do they show you? What happens to the amplitude of the oscillation when the driving frequency matches the natural frequency of the blade?
You have seen
1. That the amplitude of oscillation of the blade increases markedly when the driving frequency matches the natural frequency of the blade.
Practical advice
This quick and effective activity gives a clear example of mechanical resonance. Although we are concerned with a qualitative understanding of resonance, it is worthwhile encouraging students to attempt amplitude measurements as this will lead to more careful observations – they will ‘see’ how sharp the resonance peak is rather than quickly scanning through a range of driving frequencies. There are many ways of measuring the amplitude of oscillation. Three possibilities are: hanging a table-tennis ball by a thread and moving it towards the blade until the ball is seen to be pushed away, or direct measurement with a ruler behind the blade, or chalking the blade and allowing it to rub against a ruler – although this diminishes the amplitude.
The elastic cord forms a loose coupling between the vibration generator and the blade to give a ‘tug’ once an oscillation occurs.
Students could measure the natural frequency of the blade using a stroboscope. The problem with this is that the frequency is about 6 Hz, which is very uncomfortable and best avoided. It is suggested that the teacher or technician measures the frequency before the experiment and marks the value on the blade. A side arm of an inertial balance or ‘wig-wag’ can be used instead of the hacksaw blade if one is available.
Alternative approaches
Students may suggest other resonating systems for exploration.
Social and human context
Resonance effects are widespread. Students could be encouraged to look for readings and articles concerning resonance.
Be safe
|
Safety |
External reference
This activity is taken from Advancing Physics chapter 10, 340E
TAP 307- 6: Resonance of a mass on a spring
When the driving frequency matches the natural frequency of an oscillator the amplitude of oscillation can rise dramatically. This is resonance. This experiment gets you to measure how the amplitude of a mass on a spring varies as the driving frequency is changed.
You will need
Setting up
Set the apparatus up:
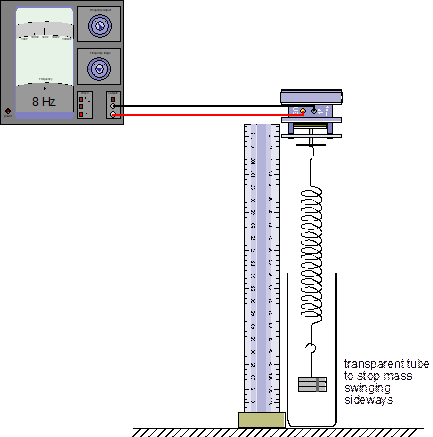
What to do
1. First of all make a careful estimate of the natural frequency of your mass on a spring and write down this value.
Next attach the mass and spring to the vibration generator and hang it in the Perspex tube. Set the variable-frequency generator at 0.5 Hz and measure the amplitude of oscillation. Repeat this at 0.5 Hz intervals up to 8 Hz. Keep a record of the results – but it is even more vital than usual to plot the results as you go, to see where extra readings are needed to define the curve.
2. Use the graph plotting package to produce a graph of your results. What do they show you? What happens to the amplitude of the oscillation when the driving frequency matches the natural frequency of the mass on the spring?
3. Now repeat the experiment with the mass suspended in water. What differences do you notice?
You have seen
1. That the amplitude of oscillation of the mass increases markedly when the driving frequency matches the natural frequency of the mass on the spring.
2. That the amplitude at resonance is smaller when the oscillation is damped than when it is undamped.
Practical advice
This quick and effective activity gives a clear example of mechanical resonance. Although we are concerned with a qualitative understanding of resonance it is worthwhile encouraging students to attempt amplitude measurements as this will lead to more careful observations – they will ‘see’ how sharp the resonance peak is rather than quickly scanning through a range of driving frequencies.
A 200g mass hanging from one spring gives a natural frequency of about 5 Hz. Two springs in series give larger amplitude but the frequency becomes rather low – showing only one side of the resonance curve.
Alternative approaches
Students may suggest other resonating systems for exploration.
Social and human context
Resonance effects are widespread. Students could be encouraged to look for articles or books that refer to resonance effects.
External reference
This activity is taken from Advancing Physics chapter 10, 350E
TAP 307- 7: Oscillator energy and resonance
A block of wood of mass 0.25 kg is attached to one end of a spring of constant stiffness
100 N m–1. The block can oscillate horizontally on a frictionless surface, the other end of the spring being fixed.
1. Calculate the maximum elastic potential energy of the system for a horizontal oscillation of amplitude 0.20 m.
2. How does the kinetic energy of the mass relate to the elastic potential energy?
3. Calculate the maximum speed of the block.
A punch bag of mass 0.65 kg hanging from the ceiling is struck and swings with a simple harmonic motion. The total mechanical energy of the oscillations is initially 55 J.
4. Calculate the maximum speed of the punch bag.
5. Describe the energy changes as the oscillations of the punch bag die away.
A drilling machine was found to vibrate so much that accurate work could not be done at certain frequencies. An investigation of its behaviour showed that the amplitude of the vibration of the drill A was related to the frequency of rotation as follows:
A / 10–2 mm |
f / Hz |
0 |
0 |
14 |
5 |
30 |
8 |
44 |
9 |
80 |
10 |
96 |
11 |
24 |
12 |
8 |
13 |
2 |
15 |
3 |
20 |
9 |
25 |
7 |
30 |
4 |
35 |
6. Draw a graph of A against f and explain its shape.
7. Why is it advisable to start to drill a hole with the drill rotating at a frequency of between 15 Hz and 20 Hz?
A bumble bee could not fly if its wing muscles had to oscillate at the same rate as its wing beat. Biochemistry makes it impossible for muscles to contract and relax as fast as this. However, the bee avoids the problem by having its wing roots embedded in a special block of elastic material.
8. Thinking of the wing as a mass and the block of material as a spring, explain how the bee’s muscle can beat at a frequency less than the wing beat.
Practical advice
This collection of questions brings together the abstract and everyday, to show the wide range of phenomena covered by resonance, connecting these with the underlying concept.
Answers and worked solutions
1. ![]()
2. The maximum E k will be the same as the maximum elastic E.
3.
![]()
so ![]()
4.
![]()
5. Energy is transferred to random thermal motions near the surface of the punch bag, in the supporting cable, and in the surrounding air. The mechanical energy of the punch bag may fall away exponentially.
6
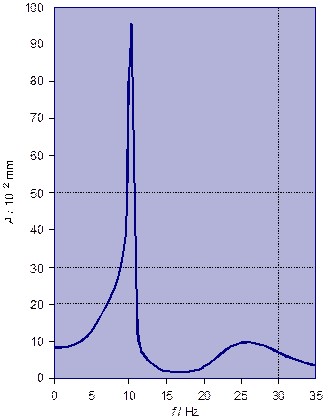
Resonance causes the drill to vibrate violently when the rate of rotation of the drill is equal to its natural frequency, around 11 Hz. The second peak occurs at approximately twice the resonant frequency, it is less sharp, possibly due to damping.
7. This is well away from the natural frequency of the drilling machine, so the drill bit will be in its equilibrium position.
8. The muscle action can be at a submultiple of the wing frequency, say f / 4. This would be like pushing a child on a playground swing only every fourth cycle.
External reference
This activity is taken from Advancing Physics chapter 10, 240S
TAP 307- 8: Resonance in car suspension systems
The background
At a simple level a car suspension system can be thought of as a mass-spring system. This means that there will be a ‘natural frequency’ at which the system will oscillate.
The spring constant
In order to work out the natural frequency of the car we need to know the spring constant of the suspension system and the mass of the car.
The frequency can then be calculated using:
![]()
1. By looking at the following sequence of photos of a car, estimate the spring constant, k, of the front spring on this car. The weight applied to one side of the bonnet of the car is around 750 N. Below: Front wheel arch of car with no extra weight on the bonnet:
Front wheel arch of car with author sitting on the wing of the bonnet:
The natural frequency
2. The mass of the car is listed in the handbook as 1120 kg. Calculate the natural frequency of the car suspension. (Remember that a car has four springs in the suspension system and therefore we can assume that the car’s mass of 1120 kg is shared equally between the four springs.)
3. If the car was ‘boxed in’ by other parked cars, describe how this information could be used to allow the car’s owner (and a few friends) to extract the car from its tight location.
Some consequences
4. Whilst driving along a particularly undulating stretch of road the driver noticed that at a speed of 70 km h–1 the car bounced up and down dramatically as it went over the humps.
Calculate how far apart the undulations in the road are likely to have been, if the effect noticed was due to resonance of the car suspension system.
You might like to try a similar calculation for your own car and then try setting it into oscillation and see if the resonant frequency coincides with the calculated value.
Practical advice
This set of questions provides a very tangible and interesting context in which to talk about resonance. But be careful not to encourage follow-up experimentation with your car, unless you are insured!
Alternative approaches
Watch a large-mass, high-amplitude, low-frequency oscillator between springs, and engage the imagination. (A dynamics trolley with 2 or 3 m of mending elastic on either side does well.
Sketch graphs of Ek against x and t, and Ep against x and t.)
Answers and worked solutions
1. The spring is compressed about 3 cm. This gives
![]()
2.
![]()
3. Bounce the car at a frequency of 1.5 Hz to get maximum amplitude bounce and gradually bounce it sideways out of the gap!
4.
![]()
and
![]()
so
![]()
External reference
This activity is taken from Advancing Physics chapter 10, 250S
TAP 307- 9: Car suspension
The axles and wheels of a car are attached to the car body by a spring suspension system in order to give the passengers a smooth ride. As the car travels over bumps in the road, the wheels follow the road surface up and down, but the much more massive car body moves more-or-less horizontally. The motion of the car wheel and axle therefore approximates to that of an oscillating mass suspended by a spring from a fixed support (the car body).
1.
(a) If you sit over the wheel-arch of a car, your weight depresses the suspension. Assuming that the suspension obeys Hooke’s law, estimate its stiffness, k. Show any other quantities you estimate or calculate in order to arrive at a value for k.
(b) If the spring suspension from (a) is used to suspend a wheel and axle whose combined effective mass is m = 100kg, what would be the approximate natural frequency of oscillation of the wheel-plus-axle?
(c) The car wheel-plus-axle system is forced to oscillate as the car goes along a bumpy road. If the bumps become closer together, or the car travels faster, the frequency of these oscillations increases. On the axes below, sketch graphs to show how the amplitude of the oscillations changes as the driving frequency changes in the case where

(i) there is little damping of the suspension and
(ii) when the suspension is heavily damped.
(d) Comment on whether the suspension system of a car should lightly or heavily damped if the aim is to give passengers a smooth ride.
Practical advice
This question provides a similar tangible and interesting context in which to talk about resonance. It does however have a different style and wording.
Answers and worked solutions
1
(a) Depression x» 5 cm (allow 2 – 10cm)
Person’s mass » 60 kg (50–90 kg), weight W» 600N
k = W/x = 600N / (5 x 10-2m) » 1 x 104Nm-1
(b) Wheel experiences restoring force, magnitude F = kx and acceleration a = -kx/m
Identify SHM with w2 = k/m
![]() = 1.6 Hz (accept 1 - 2Hz)
= 1.6 Hz (accept 1 - 2Hz)
External reference
This activity is taken from Salters Horners Advanced Physics, section BLD, additional Sheets 11 and 12
TAP 307- 10: Resonance
Resonance occurs when driving frequency is equal to natural frequency. The amplitude at resonance, and just away from resonance, is affected by the damping.
Practical advice
This diagram is reproduced here so that you can talk through it, or adapt it to your own purposes.
External reference
This activity is taken from Advancing Physics chapter 10, 140O
TAP 307- 11: Tacoma Narrows Bridge
Text to read
Engineers need to take oscillations and resonances into account when building bridges. This reading indicates what can go wrong if the static forces on a structure are accounted for, but the dynamic forces are ignored.
Tacoma Narrows
On 1 July 1940, a new bridge was opened up at the narrowest point in Puget Sound, connecting Tacoma, Washington to the Olympic Peninsula. At the time it was the third longest suspension bridge in the world. Right from the beginning, even before the construction was completed, the bridge behaved in a peculiar way. Whenever there was a slight breeze, ripples would run along the bridge. After a while local people began calling the bridge affectionately by the name Galloping Gertie. Driving across the bridge on a windy day became a favourite local pastime because it was like riding a roller coaster, although it was disconcerting to people driving across the bridge to see the car in front of them disappear over the crest of a wave.
Four months after the bridge was opened, on 7 November 1940, a new mode of oscillations showed up in the bridge in a prevailing south-westerly wind of about 42 mph. Instead of rippling motions down the bridge, twisting motions set in. The peculiarities of the bridge were being studied by a hydrodynamicist from the University of Washington, Bert Farquharson. He rushed down to take pictures of the new mode of oscillations. At 11 o'clock in the morning that day, the Tacoma Narrows Bridge collapsed. An inquest into the collapse determined that the bridge had been built according to the best engineering standards of the day. No-one was guilty of wrongdoing, but also no-one could figure out why the bridge collapsed.
A national commission investigating the collapse included Hungarian aerodynamicist Theodore von Kármán of Caltech. He explained that vortices were pouring out of the top and bottom of the deck of the bridge, driving the bridge at its resonant frequency, which eventually led to its collapse. His explanation was confirmed by experiments conducted in wind tunnels with structural models both at the University of Washington and at Caltech. In spite of the confirmation, the bridge-building community was very reluctant to accept the explanation. Why? Bridge architects were concerned with static forces. They built in brute strength to confront maximum load, water flow, wind, etc. They didn’t consider the dynamic forces. Von Kármán said that the shape the roadway presented to the wind acted like an airplane wing. The displaced air formed vortices whose action induced vibrations in the deck. Since that disastrous event, models for all major bridges have been tested in wind tunnels, and bridge engineers have been forced to consider the aerodynamics of their designs.
In the twisting mode, the centre line hardly moves at all – the vibrations go all around it.
The car belongs to a man called Leonard Coatsworth, who was a reporter on a local newspaper; he was the last person to try to cross the bridge. Farquharson himself tried to rescue a cocker spaniel from Coatsworth’s car. For his trouble, he was rewarded by the dog biting him on the hand, which was the only injury in the incident; the cocker spaniel, which never left the car, was the only fatality. A local college student named Winfield Brown decided to walk across the bridge that morning; it was a popular sport on a windy day. He came off crawling on his hands and knees, and reported one moment of sheer terror when the bridge had tilted so much under him that he looked straight down 200 ft into Puget Sound.
At the same spot there is now a new suspension bridge built with modifications suggested by von Kármán. The principal changes were to make the bridge four lanes wide, to use open side trusses, and to place ventilating grills between lanes to equalise wind pressures above and below the deck. The bridge has never had the slightest difficulty. People still look at it nervously on windy days, but it never budges.
Here are some stages in the collapse of the Tacoma Narrows Bridge on that fateful day.

Further pictures and a short video clip are available at:
http://www.enm.bris.ac.uk/research/nonlinear/tacoma/tacoma.html#file
(as at September 2005)
Practical advice
This is a straightforward reading, which students should be able to manage without help.
Further pictures and a short video clip are available at:
http://www.enm.bris.ac.uk/research/nonlinear/tacoma/tacoma.html#file (as at September 2005)
There is some debate to the exact cause but teachers may wish to look at:
http://www.engsoc.org/~leito/Billah-Scanlan.pdf It is not suggested that this article is for students.
Alternative approaches
There are many video clips showing the bridge in resonant oscillation, and the eventual collapse. One source is the Mechanics in Action video produced by the project team of the same name based at Leeds University.
Social and human context
The human-interest story here would have made it front-page journalism. The fun value of treating the oscillating bridge as being like a fairground activity, and giving it a silly name, has to be contrasted with the potential for human disaster, which fortunately did not occur. A more serious angle is the catastrophic mistake made by well-reputed engineers, and their reluctance to accept the reason for the bridge’s destruction once it had been pointed out. There is a lesson here for any physicist constructing a model which omits significant effects.
External reference
This activity is taken from Advancing Physics chapter 10, 30T
TAP 307- 12: Tacoma Narrows: re - evaluating the evidence:
Text to read
This reading is adapted from ‘The collapse of the Tacoma Narrows bridge, evaluation of competing theories of its demise and the effects of the disaster on succeeding bridge designs’ by James Koughan of the Department of Mechanical Engineering, University of Texas at Austin.
It takes further the analysis of what has become a classic example of resonance, found in almost every physics textbook. As recent reinterpretations show, the cause of this famous collapse remains a live controversy in the world of civil engineering.
The facts of the matter
The dramatic end to the Tacoma Narrows Bridge, Washington, has been a standard example of resonance used by teachers and book writers almost since the day it collapsed. Before challenging what has become accepted theory, what are the facts behind this most famous of disasters?
The Tacoma Narrows Bridge was the third longest suspension bridge in the world when it was opened in 1940. It was not a radically new design, but incorporated ideas of bridge design that had been developed over the previous ten years. The central span was 853 metres long and only 12 metres wide between the cable stays. A new method of calculating stresses (known as ‘deflection theory’) was used which allowed lighter, less expensive designs. Shallow plate girders were used on the decking instead of more traditional deep, stiffening trusses. The cables that supported the deck were attached to flexible towers which were more able to deal with changing loads than earlier designs using massive towers. All in all, the design was light, flexible and used the latest technology available.
This extreme flexibility proved to be the weakness in the design of the bridge. The vertical oscillations of the deck began soon after construction. The motion was generally considered fairly harmless and became a draw, as people came to ride the bridge. It was affectionately dubbed ‘Galloping Gertie’ as a result. On the 7 November 1940, some four months after the bridge was built, the vertical oscillations became so large that a supporting cable at mid-span snapped. The unbalanced loading created severe torsional oscillation which led to the collapse of the bridge.
The enquiry that followed the collapse decreed that the design of the bridge had been acceptable, apart from the width to length ratio. It was proposed that a replacement should be wider, despite the additional costs that would be incurred. All experts agreed that the transition from a (relatively) safe vertical motion to the destructive twisting motion was due to the slipping of a cable band to which the centre cable stays were attached. The torsional motions caused the concrete roadway to crack apart. The ‘deflection theory’ had to be addressed further with a view to examining loadings under different and dynamic as well as static conditions.
Why did the bridge collapse?
(i) The standard solution
The source of the motion of the bridge was always known to be the wind. The building up of the oscillations is seen as being due to resonance. In order for the bridge to undergo resonance, there must be a force causing the bridge to move which is periodic, regular and which matches the natural frequency of oscillation of the bridge. This effectively means that any thoughts of gusting winds being responsible can be disregarded. The gusts would have had to be very regular and this phenomenon, apart from being unlikely, was not witnessed.
The long standing theory behind the collapse of the bridge was proposed by the leading aeronautical engineer Theodore von Kármán, who was on the committee set up to study the disaster. He was convinced that the oscillations were due to the shedding of vortices from the bridge. As air flows round an object, swirls of air, called vortices, are carried away by the wind. This is due to air at different speeds combining. Consider a car with the wheels on one side driving faster than the other. The result would be the car would turn with the faster wheels on the outside of the ‘bend’. It is a common and recognised phenomena that with non-streamlined objects the vortices are shed from one side, then the other of the object (see below).
The vortices generate alternating high and low-pressure regions on the downwind side of the body, in this case the bridge. Such vortices are called Strouhal vortices and are shed at a rate determined by the equation
![]()
where fs is the frequency of vortex shedding, S is the Strouhal number (a constant for a given body shape), U is the velocity of the air flow and D is a characteristic dimension of the body (usually the width).
The characteristic dimension of the bridge was the thickness of the deck, which was 2.44 m. On the day of the collapse the wind speed was 68 km h–1 which, with an appropriate Strouhal number (developed by wind tunnel testing of many shapes over many years) gives a shedding frequency of about 1 Hz. A secondary effect would also have developed whereby the motion of the bridge would in turn generate vortices which would therefore be shed in time with the oscillations. This phenomenon is called ‘lock on’. This is the generally accepted view of how the bridge came to shake itself to pieces.
However, two researchers by the names of Scanlan and Billah pointed out in 1991 that, as the amplitude of the motion of the bridge built up, other changes to the airflow over the bridge would produce compensating, self-limiting forces. In addition, the twisting motion that, it is accepted, caused the bridge to collapse was at a frequency of around 0.2 Hz. Therefore, the collapse cannot be wholly attributed to the natural vortex shedding of the bridge structure.
Why did the bridge collapse?
(ii) New ideas
Robert Scanlan of Johns Hopkins University believes that the forces that caused the collapse were highly interactive. He claimed, in 1991, that the driving force for the oscillations was not just a function of time, as would be the case with simple vortex shedding, but was also a function of bridge angle during the oscillation. This leads to a phenomenon known as self-excitation.
According to this theory, the motion of the bridge built up to destructive amplitudes based on an intimate interaction of the wind and the structure – the wind supplying the power needed for movement and the movement supplying the power-tapping mechanism. Simply, the twisting of the bridge caused the shedding of vortices which cannot be predicted using the earlier method (the Strouhal frequency). The new flow pattern further excites the torsional mode of oscillation. The aerodynamic forces cannot affect the basic response frequencies of a massive structure like a bridge, but they can affect the damping. This resulted in the increasing amplitudes and the final destruction of the bridge.
Conclusion
As an example of resonance, the destruction of the Tacoma Narrows Bridge remains a firm favourite with educators and hopefully students at all levels. What recent studies show is that the motion of the bridge cannot be simply explained like a resonance experiment in a school laboratory. The interactions of forces, especially in a dynamic situation, become a great deal more complex. It was this that was not foreseen by the designers of the bridge in their use of new methods for lighter, flexible bridge design. However, the fact that it has been some 50 years until a more convincing theory as to the destruction of the bridge has been developed goes some way to exonerating the original designers and gives plenty of food for thought for bridge designers in the future.
Practical advice
This is a more demanding reading on the Tacoma Narrows Bridge collapse. The development of ideas concerning the subtle interactions of forces, especially in dynamic situations, may provoke discussion. Alternatively, the simple, older ideas behind the collapse of the bridge make for a straightforward resonance example. Video footage of the collapse is easily found and some measurement of frequencies, tied in to data and equations presented may be useful.
Pictures and a short video clip are available at: http://www.enm.bris.ac.uk/research/nonlinear/tacoma/tacoma.html#file (as at September 2005)
Alternative approaches
There are many video clips showing the bridge in resonant oscillation, and the eventual collapse. One source is the Mechanics in Action video produced by the project team of the same name based at Leeds University.
Social and human context
The Tacoma Bridge disaster did not result in the loss of life, but a similar collapse could easily do so. The idea of the advancement of engineering and science through pushing designs to the limit and beyond is a sometimes visited concept. The impact on bridge design after the disaster may warrant further research.
Location of resources
Adapted from Koughan J 1996 The collapse of the Tacoma Narrows bridge, evaluation of competing theories of its demise and the effects of the disaster on succeeding bridge designs (Department of Mechanical Engineering, University of Texas at Austin).
Teachers may wish to look the at the Scanlan and Billah article from the American Journal of Physics Volume 59 No.2 February 1991: http://www.engsoc.org/~leito/Billah-Scanlan.pdf . It is not suggested that this article is for students, unless they are interested.
Teachers may also like to consider the London Millenium Bridge
(These sites were available September 2005)
See:
http://www.arup.com/MillenniumBridge/
http://www.urban75.org/london/millennium.html
http://en.wikipedia.org/wiki/London_Millennium_Bridge
http://www.ice.org.uk/downloads//Millennium%20Bridge%20Report.pdf
Source: https://tap.iop.org/vibration/shm/307/file_46622.doc
Web site to visit: https://tap.iop.org
Author of the text: indicated on the source document of the above text
If you are the author of the text above and you not agree to share your knowledge for teaching, research, scholarship (for fair use as indicated in the United States copyrigh low) please send us an e-mail and we will remove your text quickly. Fair use is a limitation and exception to the exclusive right granted by copyright law to the author of a creative work. In United States copyright law, fair use is a doctrine that permits limited use of copyrighted material without acquiring permission from the rights holders. Examples of fair use include commentary, search engines, criticism, news reporting, research, teaching, library archiving and scholarship. It provides for the legal, unlicensed citation or incorporation of copyrighted material in another author's work under a four-factor balancing test. (source: http://en.wikipedia.org/wiki/Fair_use)
The information of medicine and health contained in the site are of a general nature and purpose which is purely informative and for this reason may not replace in any case, the council of a doctor or a qualified entity legally to the profession.
The texts are the property of their respective authors and we thank them for giving us the opportunity to share for free to students, teachers and users of the Web their texts will used only for illustrative educational and scientific purposes only.
All the information in our site are given for nonprofit educational purposes