Reynolds number

REYNOLD’S NUMBER
The Reynolds number perhaps is the most common dimensionless parameter used in fluid mechanics. It is defined as

• Re = ρVL/μ

where ρ is the density, V is the velocity, L is the characteristic length, and μ is the viscosity. The L term is different for each flow type. For example, for a pipe, L is the diameter of the pipe. For open channel flow, the hydraulic radius, Rh (see diagram) is commonly used.

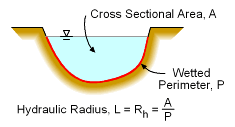
Hydraulic Radius (Used with Open Channel Flow)
Reynolds number is the ratio of inertia force and viscous force, and hence fluid flow problems where viscous forces alone are predominant. A small Reynolds number implies that the viscous effects are important, while the inertial effects are dominant when the Reynolds number is large. The models are designed for dynamic similarity on Reynolds law, which states that the Reynolds number for the model must be equal to the Reynolds number for the prototype. According to Reynolds model law, models are based on Reynolds number. Models based on Reynolds number includes:

• Pipe flow
• Resistance experienced by sub-marines, airplanes, fully immersed bodies etc.

Let
Vm = Velocity of fluid in model,
ρm  = Density of fluid in model,
Lm  = Length or linear dimension of the model,
μ m   = Viscosity of fluid in model,
and Vp , ρ p , L p , and μ p are the corresponding values of velocity, density, linear dimension and viscosity of fluid in prototype. Then according to Reynolds model law,

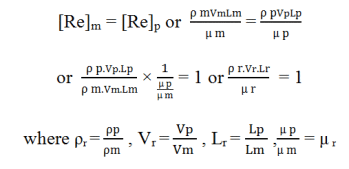
And also ρr , Vr , Lr and = μ r  are called the scale ratios for density, velocity, linear dimension and viscosity. The scale rations for time, acceleration, force and discharge for Reynolds model law are obtained as

Problem 1:
A pipe of diameter 1.5 m is required to transport an oil of sp.gr. 0.90 and viscosity 3 × 10-2 poise at 3000litre/s. Tests were conducted on a 15cm diameter pipe using water at 20. Find the velocity and rate of flow in the model. Viscosity of water at 20 = 0.01poise.
Solution.
Given:
Diameter of prototype, Dp = 1.5 m
Viscosity of fluid, μp = 3×10-2 poise
Q for prototype, Qp= 3000lit/s = 3.0 m3/s
S.p.g of oil, Sp = 0.9   ⇒  Density of oil, ρp = Sp × 1000 = 900kg/m3
Dia. of the model, Dm = 15cm = 0.15m
Viscosity of water at 20, μm= 0.01poise = 1× 10-2 poise
Density of water, ρm = 1000kg/m3
For pipe flow, the dynamic similarity will be obtained if the Reynolds number in the model and prototype are equal

Froude number
The Froude number is an important dimensionless parameter in the study of open-channel flow, and it is given by
Fr = V / (gL)0.5
where V is the average velocity, L is the characteristic length associated with the depth (hydraulic depth for open channel flow), and g is the gravitational acceleration. For rectangular cross sections, the hydraulic depth is the water depth.
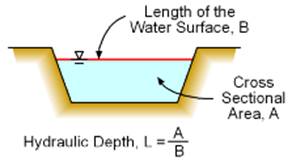(Hydraulic depth)
Physically, the Froude number represents the ratio of inertial forces to gravitational forces.
(Open channel flow)
As discussed in the open-channel sections, open-channel flow can be classified according to the Froude number in the following manner:
(a) Fr < 1: subcritical (tranquil) flow
(b) Fr = 1: critical flow
(c) Fr > 1: supercritical (rapid) flow
It is also common to write Fr as V/c, where c is the wave celerity, c (speed of a wave in the fluid). This form is similar to the Mach Number in air. For subcritical flow (V < c), the waves created by any surface disturbances (e.g., throwing a stone in the water) at the downstream can travel upstream. On the other hand, for supercritical flow (V > c), all surface disturbances will be swept downstream. The wave will remain stationary for critical flow (V = c).
According to the Froude Model Law, the Froude numbers of  the model and prototype should be equal to each other. Froude model law is the law in which the models are based on Froude number which means for dynamic similarity between the model and prototype, the Froude numbers for both of them should be equal. Froude model law is applicable when the gravity force is only predominant force which controls the flow in addition to the force of inertia. Froude model law is applied in the following fluid flow problems:

• Free surface flows such as flow over spillways, weirs, sluices, channels etc……
• Flow of jet from an orifice or nozzle,
• Where waves are likely to be formed on surface.
• Where fluids of different densities flow over one another.

Let
Vm = velocity of fluid in model,
Lm = Linear dimension or length of model,
gm = Acceleration due to gravity at a place where model is tested.
and Vp , Lp andgp are the corresponding values of the velocity, length and acceleration due to gravity for the prototype. Then according to Froude model law,

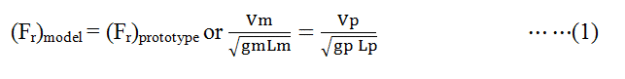
If the tests on the model are performed on the same place where prototype is to operate, then
gm = gp and equation (1) becomes as

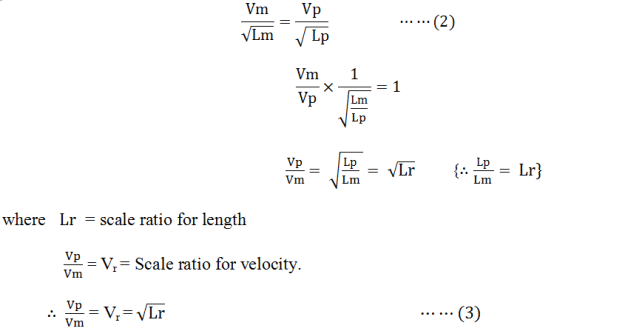
If the fluid used in model and prototype is same, then


Problem
A ship model of scale  is towed through sea water at a speed of 1m/s. A force of 2N is required to tow the model. Determine the speed of ship and the propulsive force on the ship, if prototype is subjected to wave resistance only.

As prototype is subjected to wave resistance only for dynamic similarity, the Froude number should be same for model and prototype. Hence for velocity ratio, for Froude model law using equation(3), we have

Euler’s Number (Eu)

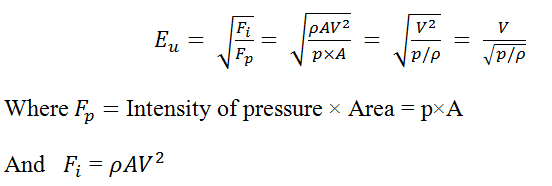
According to the Euler’s Model Law, the models are designed on Euler’s number which means for dynamic similarity between the model and prototype, the Euler number for model and prototype should be equal. Euler’s model law is applicable when the pressure forces are alone predominant in addition to the inertia force. According to this law:


Euler’s model law is applied for fluid flow problems where flow is taking place in a closed pipe in which case turbulence is fully developed so that viscous forces are negligible and gravity force and surface tension force is absent.