AN INTRODUCTION TO THERMODYNAMICS
Wayne E. Steinmetz
Chemistry Department
Pomona College
PART I. THE FIRST LAW OF THERMODYNAMICS
INTRODUCTION.
The purpose of this short discussion is to provide a correct yet understandable introduction to thermodynamics. It is intended to replace and not complement the material in your text. The author is schooled in the Oberlin school of thermodynamics developed by the faculty and graduates of the college. It is his content to convey the elegance and the utility of the subject without sacrificing rigor. The laws of thermodynamics are among the best supported in science and have far reaching consequences for all disciplines of science. Thermodynamic arguments allow one to determine feasibility of a process and the effect of external influences on the extent of a process. Thermodynamics, however, makes no statement about the rate of a process. The following important problems benefit from thermodynamic reasoning and illustrate its power: the efficiency of an air conditioner, the denaturation of a protein, the purification of an ester via distillation, the control of an enzyme, and the yield of a drug in a synthesis. In our treatment of thermodynamics, we shall give primary attention to two issues: 1) a careful, rigorous exposition of fundamental principles and 2) an understanding of chemical equilibrium.
DEFINITIONS OF THERMODYNAMIC QUANTITIES.
System. As a first step towards the development of the thermodynamic apparatus, we must define the thermodynamic system or simply the system. Following Henry Bent’s classic we use the abbreviation s for the system.1 The system (s) is the part of the entire chemical universe that is the object of the experiment. The system should be defined carefully as success in thermodynamics often depends on the choice of the system. Figure 1 shows the cartoon of a thermodynamic experiment in which the system is the gaseous contents of the piston. In this case, the system is enclosed by physical walls that do not permit the exchange of matter with the external world so the system is closed. An open system such a human red blood cell does permit the exchange of matter. The boundaries of a system do not have to be physical as in the case of the cell or the contents of the piston. They can be defined mathematically as illustrated by a small air mass.
In Figure 1, our system is immersed in a large thermal bath represented by Q. The thermal bath is normally very large compared with the system so that changes in the system will result in minor changes in the thermal bath. Our experiment in Figure 1 is designed so that the piston is connected to a system of weights. The machine will apply an external force on the system so that work will be done when the piston moves. The elements of a classic thermodynamic measurement, heat and work, are suggested in the figure.
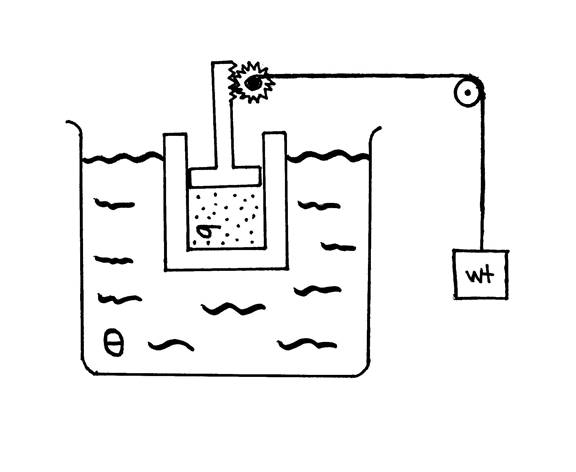Figure 1. Sketch of a thermodynamic experiment.
State. We shall approach the definition of the thermodynamic state of a system by way of an analogy. Consider the center of the Marston Quadrangle on the Pomona campus. One can uniquely and unambiguously specify the location of this point by giving its latitude (34°5.6’), longitude (117°42.7’), and elevation above sea level (1200 ft.). The location uniquely specified by the three coordinates is analogous to the thermodynamic state of a system. Suppose that our system in Figure 1 is gaseous helium at a low pressure and a high temperature so that the ideal equation of state, pV = nRT, is very accurate. If the pressure p and temperature T are fixed, the values of all intensive variables such as density, viscosity, and energy per mole are fixed. We say in this case that the state of the system is defined. We may not be able to easily calculate the values of all properties of the system but we know that setting the pressure and temperature uniquely fixes their values. Note that when the values of exactly two intensive variables is set, the state of the system is defined. The number of variables, the independent variables in a thermodynamic system, is always exactly two for a pure substance present in one phase. The number of independent variables is different for a mixture but is easily determined using a remarkable result derived by Josiah Willard Gibbs, the Newton of thermodynamics.
Intensive variable. An intensive variable is one whose value is independent of the amount of material. Temperature and pressure are two obvious examples. The intensive property of density can quickly be derived. For an ideal gas, the molar density d equals p/RT and hence is independent of the amount of material.
Extensive variable. Some quantities such as volume are directly proportional to the amount of material. They are extensive. Knowledge of the thermodynamic state also yields the values of all extensive quantities provided that one may fact is available, the number of moles.
Let us return to our analogy. The coordinates correspond to the temperature and pressure and the location, to the state. A further examination of this analogy leads to additional insights. Although one can uniquely specify the location of Marston Quadrangle with the latitude, longitude, and elevation, one could use other systems. European and military maps employ the UTM system based on a kilometer grid. The UTM coordinates replacing latitude and longitude are 3773.1 and Zone 11, 434.2, respectively. Similarly, in specifying the state of our gas, we could set the value of the temperature and pressure (the normal choices) but could have just as well used the molar volume and temperature.
State functions. Suppose we wish to travel from Marston Quadrangle to the US Forest Service Visitor Center in Baldy Village where the latitude is 34°14.4’. One can takes several routes to reach the destination. One could go directly via Baldy Road. Those desiring a wild mountain ride could rent a BMW Z3 roadster and take the Glendora Mountain Road, a classic serpentine alpine road. Iron men and women could drive to Wrightwood and then hike over Wright Mountain, Pine Mountain, Mt. Dawson, and Mt. San Antonio and finally down down down to Baldy Village. Your insane instructor has done this once but only once. The path taken for each of these excursions is quite different but the change in latitude, 9.8’, is exactly the same. In other words, the value of the change in latitude is independent of the path. Any function that displays this path independence is called a state function. Note that the state functions latitude, longitude, and elevation are used to specify location. Similarly, temperature and pressure are examples of state functions. Since they are used to define the thermodynamic state of a system, they are called thermodynamic state functions. We shall endeavor whenever possible to work exclusively with state functions since the property of path independence is so useful Path independence is a very important component of a full statement of the laws of thermodynamics as we shall soon see.
THE FIRST LAW OF THERMODYNAMICS.
Before we proceed with a careful exposition of the First Law, we shall go directly to a succinct but full statement of the powerful result. The First Law comes in two parts.
The first makes a statement on how energy charges are made; the second, on an important mathematical property. Both parts are required.
I) DE = q + w.
II) DE is path independent.
The author has deliberately not used familiar dictionary statements of the First Law (“energy is neither created nor destroyed” or “Die Energie der Welt ist konstant”) which are results derived from the First Law and notthe First Law. Be wary of confusing postulates with corollaries!
As part of your general education, I have slipped in the text of Clausius’ famous paraphrase of the First Law in the original German.
Heat. The statement of the First Law refers to two quantities q (heat) and w (work). We must define these carefully in order to fully understand the First Law and use it properly. We shall start with heat. As a first step, you may have to revise some misconceptions. Heat as discussed on the street is often not the same as thermodynamic heat. Heat is defined by an operation which is very simple but for many counterintuitive. Heat is an indicator of change. If the state of the system does not change, the heat is exactly zero. The converse does not follow. If the system is perfectly insulated from any thermal bath, the heat is also zero. We call such a process adiabatic.
Consider a non-adiabatic process. The system is immersed in a thermal bath Q and a change in the system results in a temperature change of the thermal bath, DTQ . The change in the temperature of the thermal bath is definitive; if it is zero, the heat is zero. Given a non-zero value of DTQ, the value of the heat of the thermal bath is given by
qQ = CQ DTQ (1)
where CQ is the heat capacity of the thermal bath. Recall that the thermal bath is normally large so that DTQ will be small. (We shall not deal with exceptions in this document. The full story is usually told in a course in Physical Chemistry.) Equation (1) yields the heat of the thermal bath. The desired system heat, qs, is easily obtained from qQ. The heat of the thermal bath and the system heat are equal in magnitude but opposite in sign.
qQ = CQDTQ = -qs (2)
Example 1.
Problem. First Aid kits frequently contain cold packs that consist of a bag two compartments, one filled with pure water and the second with potassium nitrate. When a cold surface is required, the user breaks the seal separating the two compartments and the salt dissolves in the water. A technician wishes to characterize the product. In one experiment, the system is 0.00200 mole (0.202 g) of crystalline potassium nitrate initially at 25.00°C and the process is dissolving it in 100.0 mole of liquid water which is also initially at 25.00°C. The water serves as the thermal bath. As a result of the mixing, the solution drops in temperature by 0.0093°C. Calculate the system heat.
Answer. We require the heat capacity of the water in the solution. Since the solution is dilute, we shall use the heat capacity of pure liquid water. Since heat capacity is an extensive quantity, the heat capacity of 100.0 moles of pure liquid water is obtained by multiplying the number of moles of water, 100.0 mole, by the molar heat capacity of liquid water at 25.00°C, 75.291 J/K-mole. The heat calculation readily follows.
CQ = (100.0 mole)(75.291 J/K-mole) = 7529 J/K
\ qs = -qQ = -(-0.0093 K)(7529 J/K) = 7.0 x 101 J
Discussion. This assignment of system and thermal bath is the same as that in the measurement phase of the Enthalpy of Solution experiment. The temperatures are given in Celsius which are not the same as the values in Kelvin. However, since the Celsius and Kelvin scales differ only by an additive constant, temperature changes are the same in the two systems of units. Note that the heat capacity of the potassium nitrate is not required in this problem. A foxy instructor might provide the number on an exam as a decoy. Often in water problems, the amount of water is given in grams. One could convert mass to moles or use the specific heat of liquid water, i.e. its heat capacity on a gram basis. The number is (75.291 J/K-mole)/(18.0154 g/mole) = 4.1793 J/K-g. If one converts this to calories, one obtains a number very close to one. This is no accident. Liquid water is the basis for many features of our present system of units. Finally, note that the sign of the system heat is positive
Example 2.
Problem. A 1:5 mixture of methane and dry air is ignited in a Bunsen burner. Calculate the system heat immediately, e.g. one microsecond, after ignition. The system is defined as the gases and the products of their combustion.
Solution. This could be a very nasty problem if the problem were defined differently. However, the solution is trivial if one knows one result from physics. The transfer of thermal energy is relatively slow and is especially slow for gases which have a very low density. The is no time for the transfer of thermal energy to the thermal bath, the air surrounding the flame, so the process is adiabatic.
Discussion. The problem was set up to trap those who refuse to base their analysis on fundamental principles and instead rely on vague recollections, street knowledge, or the nearest formula. Those untrained in the principles of thermodynamics will be surprised by the result as they erroneously associate heat with a temperature change in the system rather than the surroundings.
The problem might appear to be trivial but it is not. The adiabatic condition at the point of ignition is the basis for a straightforward calculation of the calculation of the temperature at this point. This is the hottest part of the flame that appears as an inner blue tip in the Bunsen-burner flame. After the hot product gases flow from the site of ignition, they have time for exchange of thermal energy with the environment. The surrounding air increases in temperature and the product gases drop in temperature. Over a longer time scale, heat is not zero! The system heat is negative since the surroundings increase in temperature.
A sign convention for heat that follows from equations (1) and (2) is presented in the two examples. Positive system heat follows from a drop in the temperature of the thermal surrounds; a negative system heat, from an increase. One cannot draw inferences from the sign or even existence of heat from the temperature change in the system. Furthermore, note that the terms exothermic and endothermic are NOT, definitely NOT associated with the sign of heat. These terms are tied to the sign of the change of the enthalpy function. This point will be made again in the section on enthalpy.
Work. We noted with some emphasis that the system heat or simply the heat is indicated by a change in the temperature of the thermal surroundings external to the system. A similar situation applies to the definition of thermodynamic work. Non-zero thermodynamic work requires two elements: extension and an external force. The simplest example of work is pressure volume work illustrated by the piston in Figure 1 in which the volume of the gas either expands or decreases under an external pressure applied by the piston. Treatments of thermodynamics give primary attention to this type of work for two reasons. Calculations in the gas phase are relatively simple and expansion-compression processes provide the basis for the form of the equilibrium constant expression. The expression for system work is
ws = -pextDV (3)
where pext is the external pressure and DV, the change in the volume of the system, is the extension. A general sign convention for work is implied by equation (2) and can always be kept straight by referring to the example of a piston. Consider compressing a gas (air) with a bicycle pump. It requires effort on your part to reduce the volume of the air. Note that DV is negative and the work therefore is positive. On the other hand, consider the piston in an automobile where a chemical reaction in the system is used to derive useful work. The mixture of octane and air are ignited in the piston. The hot product gases expand against a large external force presented by the drive train of the car. Here DV is positive and the work is negative.
Example 3.
Problem. Two moles of a gas are present in a piston and initially occupy a volume of 5.0 liter. Quickly additional weights are applied to the piston and the external pressure is suddenly increased to 4.0 atm. Under this increased pressure, the gas decreases in volume to a final volume of 3.0 liter. Calculate the system work.
Solution. The volume change or V(final) – V(initial) is 3.0 liter – 5.0 liter - -2.0 liter.
\ws = -pextDV = -(4.0 atm)(-2.0 liter) = 8.0 liter-atm = 8.1 x 102 J
Discussion. Note that the sign of the work is positive. The external world had to be applied to effect the compression. The compression would not occur spontaneously without the increase of the external force on the piston.
Your instructor is a practical fellow who uses SI units when expedient but prefers to use non-SI units, namely volume in liters and pressure in atm, in most gas-law calculations. The old approach is simply more convenient. However, once the calculation has been completed, the result in liter-atm should be converted to Joule by the conversion factor 101.325 liter-atm/Joule.
This example was provided to introduce the concept of thermodynamic work. The instructor has no intention of loading you with the full range of work calculations. (He will deliver the full dose in Physical Chemistry.) There are several ways to perform the problem but the solution makes full use of fundamentals. Note that lots of information is not used: the number of moles of the gas, the actual initial pressure, the temperature of the gas. None of these details are needed in this problem. In some work problems, one uses everything. You will be spared these details in General Chemistry where the primary focus is on chemical reactivity.
The conditions were changed quickly in this problem and the response was significant. The volume changed by 40%. This is a clear example of what thermodynamicists call an “irreversible” change. This term is slippery and a full grasp requires a deep understanding of the mathematical limit. Unfortunately, kineticists define it differently. We shall return to this idea in the unit on entropy. For now, as you are wearing your thermodynamicist’s hat (in Yale blue), think fast, big changes, not slow, incremental changes when you hear irreversible.
Example 4.
Problem. George Kistiakowsky at Harvard pioneered the use of the shock waves in the study of fast reactions. Consider the following adaptation of one of his instruments. A tube consists of two compartments that are separated by a thin metal diaphragm. The first compartment which contains a moveable needle is filled with oxygen at 2500 atm. The second compartment is evacuated. In the experiment, the needle punctures the diaphragm and the high pressure gas expands to fill the evacuated compartment. Calculate the work if the system if the gas.
Solution. There is no work. There is extension but there is no external force. The internal force of the gas does not count in this case.
There are many types of forces and nature and hence types of thermodynamic work. We shall often divide the work into two types: w(p-V), pressure-volume work and w(other), everything else. In General Chemistry, we shall consider only one type of w(other), electrical work as it is of primary importance in electrochemistry. In this case, the extension is the flow of charge Q, and the external force is a potential difference, V. (V, often simply called the Voltage, is often symbolized by electrochemists as E.) In magnitude, electrical work is given by
w(electrical) = QV (4)
If we are operating with direct current, Ohm’s Law ( V = IR) applies. If the current is constant, Q = It. If these two conditions apply, equation (4) simplifies to
w(electrical) = I2Rt (5)
In this case, the student is recommended to use SI units. Charge, Q, is given in Coulomb; current, I, in Ampere or Coulomb/second; Voltage, V, in Volt; resistance, R, in Ohm; and time, t, in second. Note that a Volt-Coulomb is a Joule, the SI unit of energy.
An Experimental Exposition of the First Law. Physical chemists take great care in the development of fundamental principles and always begin with a simple but well designed system; The system in the following Gedanken experiment is a bar of pure
Gedanken is German for a thought experiment. The grand master of Gedanken experiments was the Swiss-American physicist Albert Einstein.
solid, copper. Recall for a pure substance in one phase with fixed mass that exactly two state functions or variables define the state of the copper. I shall make the conventional choice of pressure and temperature. If the experiment is conducted on an open bench, the constant atmospheric pressure maintains a constant pressure. Therefore, in this Gedanken experiment, the energy E of the copper depends solely on temperature. These simplifications (not approximations!) result in the following simple relationship:
DEs = CsDTs (6)
Armed with this result, we can perform the following set of experiments. In each one, we shall employ different methods to increase the temperature and hence the energy of the copper by the same amount.
In the first experiment, the temperature of the copper (the system, s) is increased by DTs by dipping it in a hot oil bath (the thermal bath, Q) with a known heat capacity CQ. The system heat, qs, is obtained by applying equation (2) to a measurement of the temperature change of the thermal bath. Similarly, the energy change of the system, DEs, is determined via a separate and independent calculation from equation (6) and DTs. When one compares the two results, qs and DEs, one finds that they are equal within experimental error. Note that no external forces have been applied to the system in this first experiment and the system work is zero.
Work is performed in the second experiment by connecting the ends of the copper bar to a battery until its temperature increases by DTs. The system work, ws, is obtained from equation (5) and the values of the Voltage, the time of resistive heating, and the resistance of the copper. A high-Voltage battery is used so that the temperature increase is achieved before the copper bar is able to transfer thermal energy to the environment. That is, the second process is adiabatic. When one compares the two results, ws and
DEs, one finds that they are equal.
In a third series of experiments, the copper bar is increased in temperature by DTs by a combination of the two methods: dipping in the oil bath and connection to the power supply. In this third case, both the work and heat have non-zero values but neither equal DEs. However, one finds that their sum does, i.e. DEs = qs + ws.
Several important results can be derived from this series of Gedanken experiments:
The conclusion that energy is a thermodynamic state function has not been obtained deductively but rather was inferred via induction from the results of the Gedanken experiment. The results of this single experiment, however suggestive, are not sufficient to establish the validity of the inference. This remarkable result has been tested many times and with many systems and the experimental results have always been in agreement with the inference. Consequently, the conjecture has been elevated to the status of a scientific Law, a designation reserved for a well supported result that has broad implications. This Law known as the First Law of Thermodynamics and its importance in science and technology justifies a restatement:
I) DE = q + w.
II) DE is path independent.
Some comments are in order before we move on to applications of the First Law. Note that the First Law establishes a relationship between heat and work and an energy change, not with energy. That is, energy is not heat plus work. In fact, there is no method of measuring absolute energies; experimental data only yield changes in energy. An interesting result follows from the First Law for the case where the system is the entire universe. Since there is nothing physical that is external to the universe (no external forces and no external thermal bath), the heat and work of the universe are both zero. Consequently, by the first part of the First Law, the change in energy of the entire universe is zero for any change in the universe, however dramatic. This result is often proclaimed as the First Law. It is not; it is simply a result derived from the First Law.
Example 5.
Problem. A common meteorological condition in Southern California is a Santa Ana. Winds from the desert clear the air and yield high temperatures in the valleys and low temperatures in the mountains. What is the thermodynamic basis for these temperature effects?
Solution. We shall define our system as a small air mass containing N molecules. The actual size of the air mass is not important since we are interested in temperature, an intensive state function. Gases are dilute and consequently serve as good thermal insulators. Furthermore, when the winds are present, the air masses move quickly. Consequently, the rate of thermal energy transfer is very slow compared with the rate of transfer of air masses over the mountains. In other words, we can treat the process as adiabatic. In this problem of mass transfer, the pressure applied on our system is the atmospheric pressure. Barometric pressure decreases as one rises in elevation. Hence, the volume of the air mass will increase with an increase in elevation and decrease with a decrease in elevation. From equation (3) we can readily conclude that the system work is negative for expansion and positive for compression. From the First Law, one infers that the energy change equals the system work with the necessary result that the energy decreases with a rise in elevation and increases with a drop in elevation. The tie to temperature comes with equation (6). In the case of ideal gases, the energy is completely independent of pressure and volume. Therefore, if the gas is inert (no phase changes and no chemical changes), the energy depends only on temperature. Consequently, the temperature drops as the air mass rises and increases as it drops into the Pomona Valley. Thermodynamics resolves the apparent contradiction. When the Santa Ana winds are strong in late August, one can almost fry an egg on the streets in Claremont but will be unpleasantly cold on the summit of Mount San Antonio.
Discussion. Armed with calculus, one can handle this problem quantitatively and obtain a numerical value for the change in temperature with elevation. This is the thermodynamic lapse rate and is -9°C/km for dry air.
The Meaning of it All. We have provided an operational definition of heat and work which is the only legitimate approach. Many experiments dealing with heat and work provide the empirical basis for the First Law whereby an energy change is tied to the sum of heat and work. Many students are not satisfied with this approach and their question “What is thermodynamic energy?” is in fact the request “Please provide me with a molecular interpretation.” This request is legitimate but must be approached with caution as many textbook explanations are simplistic and misleading. The discussion here will proceed far enough to address your concerns but will avoid difficult mathematics and logical traps.
According to the atomic-molecular model, a sample of a pure substance contains vast numbers of molecules. The molecules are identical in terms of covalent structure, the order in which the atoms are connected, but will differ in the state of molecular agitation. Consequently, the thermodynamic energy (sometimes called the internal energy U) is an average over many molecular states. For a type of molecule, there is a set of accessible molecular energy states, each with an energy Ei. Each value of Ei is the total energy that a single molecule can possess and quantum-mechanically is a well-characterized quantity. (We shall not divide Ei into potential and kinetic energies; at the level of General Chemistry this separation raises theoretical conundra that do not inform our knowledge of chemistry.) Out of the total N molecules in the sample, Ni molecules will be present in each state i. The value of Ni can change with temperature. The observed thermodynamic energy is a weighted average with a very small standard deviation for large N.
E = åNiEi (7)
It is safe to stop here. The next step requires a careful development
that is presented in advanced courses. This instructor will refrain from providing a molecular interpretation of heat and work as they are path-dependent quantities. A legitimate molecular interpretation is only possible if constraints are placed on the system and the processes. We shall refrain from such speculation as our goal is understanding reaction chemistry and laying a sound framework.
ENERGY CHANGES AND CALORIMETRY
At this point, we shall shift our attention from the development of general fundamental thermodynamic principles to a particular application, chemical equilibrium. We shall soon see that the value of an equilibrium constant has contributions from two properties of molecules: their energy and their symmetry. The need for understanding chemical equilibrium and accurately calculating equilibrium constants is our primary motivation for our study of energy changes. We shall start with an examination of experimental methods and then demonstrate how energy changes can be obtained from tabulated data.
There are three primary routes to the experimental determination of energy changes. First, one can calculate them directly by employing methods of quantum mechanics. This approach which will be examined later works best for small molecules in the gas phase and at best yields results with an uncertainty of several kiloJoule. Energy changes for reactions can be related to molecular dissociation energies. In a few special cases such as oxygen and nitrogen, very accurate values of gas-phase dissociation energies can be obtained from spectroscopic data. The best and often the only source of accurate energy changes is calorimetry, the art of measuring heat.
If care is taken, heat can be measured accurately and precisely. However, heat is a path-dependent quantity and the result depends on the details of the process. Fortunately, one can devise experiments in which the heat equals the change in a thermodynamic state function. Then one has the best of both worlds, an accurate result and a path-independent quantity. The first experimental realization is the bomb calorimeter in which the reaction, often a combustion reaction, is performed inside a sealed vessel, the bomb. During the run, the bomb is immersed in a large water bath. In this arrangement, the contents of the bomb constitute the system (s) and the bomb itself plus the water bath constitute the thermal environment (Q). The bomb normally is made of thick gun steel and maintains a constant volume. Therefore, the pressure-volume work is zero even though the external pressure applied on the system is not zero.. If the experiment is designed so that no other external forces are present, the total system work is zero and consequently the system heat equals the energy change. In short,
DE = q if DV = 0 and w(other) = 0 (8)
Example 6.
Problem. A team of chemists are designing a small backpacking stove and wish to measure the fuel value of liquid isobutyl alcohol (C4H9OH). They plan a determination of its energy of combustion, i.e. the energy change for the combustion reaction
C4H9OH(l) + 6 O2(g) --> 4 CO2(g) + 5 H2O(l)
To this end, they load a calorimeter bomb with 0.5654 of liquid isobutyl alcohol, an excess of gaseous oxygen, and 1.00 ml of liquid water. They insert the bomb in a water bath initially at 25.00°C, initiate combustion in the closed bomb, and observe that the temperature of the water bath increases by 2.231°C. In a separate, calibration experiment, they charge the bomb with oxygen, water, and 1.0985 g of benzoic acid for which the energy (change) of combustion is -22968 J/g. As before, the bomb is immersed in the same water bath. Following ignition, the temperature of the water bath increases by 2.851°C. Determine from these data the molar energy of combustion of the isobutyl alcohol.
Solution. First we require the heat capacity of the calorimeter (Q). The combustion of the benzoic acid is expected to yield an energy change of (-22968 J/g)(1.0985 g) = -25230 J. Since a constant-volume bomb calorimeter with no w(other) is used, the energy change equals system heat, qs, which in turn equals -qQ and therefore -CQTQ. The required heat capacity is given by
cQ = -DEs/DTQ = -(-22968 J)/(2.851°) = -8849.6 J/°C.
With the heat capacity CQ in hand, the process is reversed and the energy change for the combustion of the isobutyl alcohol is readily calculated.
DEs = qs = -qQ = -CQDTQ = -(8849.6 J/°C)(2.231°C) = 19744 J
The sample size, 0.5654 g, corresponds to (0.5654 g)/(74.12 g/mole) = 0.007628 mole so the molar energy (change) of combustion is (-19.744 kJ)/(0.007628 mole) = -2588 kJ/mole.
Comments. Several tricks in the art of calorimetry are worthy of mention. The bomb is loaded with an excess of liquid water to guarantee that all the water from the combustion is produced in the liquid state. With an excess of water, a state of 100% relative humidity applies in the bomb. Water has reached its maximum vapor pressure and any water produced in the combustion reaction must appear as liquid. An accurate measurement of the heat requires perfect or near perfect insulation of the calorimeter from the environment. To this end, one inserts the calorimeter in a second water bath that is always maintained with a manually or computer-controlled heater at the same temperature as the inner water bath. The rate of thermal energy exchange between two bodies is directly proportional to the their temperature difference. If the latter is zero, the rate is zero and perfect insulation results. This clever trick is counterintuitive since close contact between two objects is usually a recipe for poor insulation. Note that the initial temperature of the apparatus is given. This is important as energy changes have a small but not insignificant dependence on temperature. That is, the change in DE over the range 1-2 K is less than the experimental error and can be ignored. However, the same quantity at 100°C will differ measurably from the value at 25°C. Hence, a full statement of the experimental result would be the energy of combustion of liquid isobutyl alcohol at 25°C was found to be -2588 kJ/mole. Large negative values of DE are typical for combustion reactions.
Finally, bomb calorimeters are routinely used to determine the caloric value of foodstuffs. Organisms employ a very indirect pathway for combustion but the outcome is the same as with a bomb calorimeter. Accurate measurements with organisms are very difficult and routine with bomb calorimeters. We are assured by the First Law’s claim of path independence for energy changes that the two results
Many reactions are conducted on the laboratory bench and the constraint of constant pressure (achieved by atmospheric pressure) rather than constant volume applies. In this case, the heat equals a change in a thermodynamic state function when only pressure-volume work is performed. The required state function is a new state function, enthalpy which is represented by H. H is defined as follows:
H = E + pV (9)
Note; p in the defining equation is the internal pressure, the p in the ideal equation of state, and not the external pressure. A sign convention exists for enthalpy changes. A process with a negative enthalpy change is exothermic; with a positive change, endothermic. Enthalpy has several very important properties. First, since it is defined in terms of thermodynamic state functions, it is a state function and therefore enthalpy changes are path independent. It also is what we require for calorimetry run under constant pressure conditions as the following algebraic steps will show. For any process, it follows from equation (9) that
DH = DE + pDV + VDp. (10)
If the First Law is invoked, equation (10) becomes
DH = q -pextDV + w(other) + pDV + VDp (11)
where the usual division of work into pressure-volume work and other work has been made. Equation (11) is a general cumbersome result but it greatly simplifies if the constraint of constant volume is made. An important consequence of constant pressure is the equivalence of the external pressure, pext, and the internal pressure, p. As a result, the second and fourth terms cancel, the fifth term is zero, and equation (11) becomes
DH = q + w(other) (constant p) (12).
If the experiment is conducted not only under the constraint of constant pressure but also with the exclusion of other types of work, the second term in equation (12) vanishes and then the heat equals the enthalpy change. These are the conditions for the calorimetric measurement of enthalpy changes that will be employed in the Enthalpy of Solution experiment. Both these conditions often apply but careless writers and students often neglect the requirement that pressure-volume work be the only form of work. This important requirement is satisfied when two reagents are mixed in a flask but is not satisfied in a battery or in human muscle. In these latter very important examples, both terms in equation (12) apply.
As in the case of energy, the question “What is enthalpy?” inevitably rears its head. The formal answer refers to the definition: H = E + pV. This answer, although complete, is hardly satisfying as enthalpy is an abstract quantity. A somewhat fuzzy, but more satisfying answer is to associate enthalpy with energy. This identification follows from the definition with one qualification. First consider the enthalpy of a substance in a condensed phase. The molar volume in this case is fairly small as the molecules are densely packed. Unless the pressure is high (a condition that will not be examined in this course), the product pV is normally quite small and therefore H and E can be used interchangeably. This is not the case for gases. However, the ideal equation of state identifies the product pV with nRT and H simplifies to E + nRT. In most cases nRT will be small compared with E but not so small that it can be completely neglected. In summary, the question “What is enthalpy?” can be succinctly answered with the following set of equations.
H @ E (materials in condensed phases) (13)
H = E + nRT (gases)
Example 7.
Problem. The preceding discussion leads to a sequel to Example 6. Stoves normally function with the flame open to atmospheric pressure. Although the chemists obtained a value for the energy change, they really need a value for the enthalpy change. They made the right measurement; accurate calorimetry is best done in a bomb calorimeter. A conversion of their value of DH into DE is needed.
Solution. If all else fails, go back to definitions. From H = E + pV, it follows that DH = DE + DpV where the difference for a quantity means its value at the end minus that at the beginning.
DpV = pV(H2O(l)) + pV(CO2(g)) – pV(O2(g)) – pV(C4H9OH(l))
Following the lead of the above discussion, we’ll discard the pV product of species in condensed phases and replace it with nRT for gaseous species. Per mole of isobutyl alcohol, we obtain
DpV = 4RT – 6RT = -2RT and
DH = DE - 2RT = -2588 kJ/mole –2(8.315 J/K-mole)(298.15 K)
= -2593 kJ/mole
Discussion. This conversion was done not simply to illustrate a point of theory. Experimental work usually produces an accurate energy change but a calculation of an equilibrium constant requires an enthalpy change. The adjustment to DE is relatively small. This is normally but not always the case. The small size justifies the approximations made. A small error to a small quantity is very small and can be neglected. Note in this case that the result was derived as needed. The instructor has a great aversion to the use of memorized formulae.
THE USE OF STANDARD ENTHALPY CHANGES
The practice of science is the development of models and this enterprise involves the acquisition and analysis of data. It might come as a surprise but most chemical data used in science does not come from the laboratory but instead from the library. The important point of this section is the intelligent use of the massive databases of published experimental data. As an example, consider the following reaction for the production of ethane from acetylene.
HCºCH(g) + 2 H2(g) --> C2H6(g)
We shall apply thermodynamic reasoning in this case to the determination of enthalpy changes but the approach can be applied to any thermodynamic state function. In developing the approach, we shall divide the net reaction into a set of reactions which when combined would yield the net reaction. We shall utilize the path independent feature of enthalpy.
We also require an additional result that applies for any thermodynamic state function, X: the value of DX for the forward reaction is -DX for the reverse reaction. To see this, consider a reaction A-->B for which DX is DX(forward). The reverse process is the reaction B-->A with DX(reverse). Add the two reactions; the net result is no reaction at all. We are back where we started and DX(net) must be zero. Due to path independence, DX(net) is the sum of the DX’s for the two steps.
0 = DX(net) = DX(forward) + DX(reverse)
\ DX(forward) = -DX(reverse)
The utility of tabulated data will be illustrated by an analysis of the above reaction. The net reaction can be broken up into several steps where in each step a reactant is converted into the chemical elements or a product is formed from the chemical elements.
Step I: HCºCH(g) --> 2 C(s) + H2(g) DH(I) = -DHf(HCºCH(g))
Step II: 2 H2(g) -->2 H2(g) DH(II) = 0 [H2 is an element.]
Step III: 2 C(s) + 3 H2(g) --> C2H6(g) DH(III) = DHf(C2H6(g))
Net: HCºCH(g) + 2 H2(g) --> C2H6(g) DH(net) = DHrxn = DH(I) + DH(II) + DH(III)
= DHf(C2H6(g)) -DHf(HCºCH(g))
The net reaction could be completed by the sequence of the three steps and the enthalpy change for the net reaction is equal to the sum of the enthalpy changes for the separate steps. This step depends on the path independent property of enthalpy. Chemically, the third step is the formation of the product ethane directly from the elements. Instead of labeling the enthalpy change as DH(III), we can use the more descriptive term DHf(C2H6(g)), the molar enthalpy change of formation of gaseous ethane from the elements or simply the enthalpy of formation of gaseous ethane. Similar, the first step is the reverse of the formation of acetylene and therefore DH(I) is -DHf(HCºCH(g)), minus the enthalpy of formation of gaseous acetylene. The final result which is given in the slightly rearranged form is instructive. The overall enthalpy change for the reaction is the sum of the enthalpies of formation of the products minus the sum of enthalpies of formation of the reactants. Note that we require a weighted sum where the weights are given by the stoichiometric coefficients. This important result is generalized in equation (14):
for the reaction a A( ) + b B( ) + ... --> x X( ) + y Y( ) + ... (15)
DH = DHrxn = xDHf(X) + yDHf(Y) - aDHf(A) - bDHf(B)
Before we can apply equation (15) and obtain the enthalpy change for the hydrogenation of acetylene, we need to discuss a thermodynamic convention used in the tabular data. The convention is a consequence of the fact that absolute energies and therefore absolute enthalpies are not achievable. We can only determine enthalpy and energy changes. However, the preparation and use of databases is greatly simplified if we act as if absolutes were possible. This is not a swindle but the use of a convention. No trouble results if everyone agrees to use the same convention at all steps in the calculation.
The utility of conventions is illustrated by time. There is no absolute time but navigation is greatly simplified by the acceptance of a standard. Every US Air Force base has at least two clocks. One displays local time and the other ZULU time (Greenwich Mean Time for the British subjects in the class). All world governments have agreed to base their clocks on the setting of local noon in Greenwich. The values of longitude on maps are based on a similar convention which places THE great circle with longitude zero exactly through the Royal Observatory in Greenwich.
The following convention is used in tabulations of thermodynamic data:
The standard enthalpy of formation of an element in its most stable form is zero. The standard enthalpy of the hydronium ion in water is also zero. Standard conditions are indicated by a degree superscript, e.g. DHf°
If you read the statement carefully, you will note the qualifier standard which must be defined. Enthalpy and energy exhibit a very small dependence on concentration. Entropy, a state function to be introduced with the Second Law, has a strong dependence on concentration. Therefore, our convention must set the enthalpy of formation to zero under specified conditions of concentration and pressure. These conditions are referred to as standard conditions. Thermodynamicists have agreed on the following statement of standard conditions:
(There was a change in the standard state in 1982 based on a conversion from atm as the unit of pressure to Pascal. The standard pressure of 0.1 MPa whereas 1 atm is exactly 0.101325 MPa. Note that the two are almost the same. It is quite convenient to retain the atmosphere as the unit of pressure and ignore the error that results. In most cases, the error is negligible. We shall use the atmosphere in General Chemistry.)
Consider a few examples. At atmospheric pressure and 298.15 K (25.00°C), the most stable form of molecular iodine is crystalline iodine so the standard enthalpy of formation of crystalline iodine , DHf°(I2(s)), is zero. The standard enthalpy formation of iodine in other phases will be non-zero. For example, the standard enthalpy of formation of gaseous iodine is 106.838 kJ/mole at 298.15 K. From these two numbers, we can readily determinate the standard (i.e. under standard conditions) enthalpy change for the sublimation of iodine. The process is I2(s) --> I2(g) so DH° = DHf°(I2(g)) - DHf°(I2(s)) = 106.838 kJ/mole – 0 = 106.838 kJ/mole. The element sulfur is an interesting case. It has several crystalline forms. Under standard conditions, rhombic sulfur is the stablest form under 368.54 K; above 368.54 K, monoclinic sulfur is more stable. Hence, at 298.15 K, the standard enthalpy of formation of rhombic sulfur is zero but at 370, it is non-zero.
Under the conditions that we normally encounter in General Chemistry, energy and enthalpy do not depend measurably with concentration so there are no consequences to ignoring the concept of standard states. Do not develop this bad habit as entropy, the most important state function, does depend on concentration and the neglect of standard states has serious consequences.
You will note in many textbooks and databases that thermodynamic data are given at 25.00°C (298.15 K). This is a convenient reference temperature as it is close to ambient temperature and the physiological temperature. In spite of what you may have been taught elsewhere, there is NO standard temperature. In this course STP is a brand of motor oil! Enthalpy and energy do depend on temperature and their temperature dependence is tabulated in the more comprehensive databases. Fortunately, the variation of enthalpy and energy changes with temperature is usually small and we shall ignore the effect in General Chemistry.
After this long but necessary digression, we are finally in a position to calculate the enthalpy change for the hydrogenation of acetylene. We’ll use data at 298.15 K and explicitly cite the temperature as it matters. We’ll also calculate the enthalpy change under standard conditions and thus avoid a long gauntlet of daunting calculations that make a miniscule contribution to the final result. That is, the number under non-standard conditions will be very, very close to that calculated.
DHrxn = DH°(298.15 K)
= DHf°(C2H6(g), 298.15 K) -2DHf°(H2(g), 298.15 K) - DHf°(HCºCH(g), 298.15 K)
= (1 mole)(-84.68 kJ/mole) – (2 mole)(0 kJ/mole) – (1 mole)(226.73 kJ/mole)
= -311.41 kJ
This concludes a proper thermodynamic calculation in which we have crossed all our t’s and dotted all the i’s. Care has been taken to specify the temperature and the physical state (i.e. the phase) of the reactants and products. The next example will illustrate the need to provide the phase information. Thermodynamics is a subject that can reward diligence but discipline is needed to produce credible results. As a final step of this or any real problem, we should attempt to learn some chemistry from an analysis of the result. We are teaching thermodynamics because it is a beautiful subject but also because it informs our understanding of the chemistry. Note that the enthalpy change is large and negative. The acetylene seems to be the major source of the number. Its standard enthalpy of formation is large and positive. Most compounds have a negative enthalpy of formation. Acetylene’s positive enthalpy of formation indicates that it is a very reactive compound and must be used with great respect.
Chemists have learned that the solvent can greatly influence the extent and also the outcome of a chemical reaction. Acetylene and ethane are non-polar compounds and are not very soluble in water but they have a limited solubility. The thermodynamics of our hydrogenation reaction in water are worthy of study as the results might provide a better understanding of the role of the solvent. Hence, we need the enthalpy change for the reaction
HCºCH(aq) + 2 H2(g) --> C2H6(aq)
Note the subtle but as we shall see significant changes. The hydrocarbons are present in the water phase and not in the gas phase. We could solve this problem in the same way as the previous one, namely
DHrxn = DH°(298.15 K)
= DHf°(C2H6(aq), 298.15 K) -2DHf°(H2(g), 298.15 K) - DHf°(HCºCH(aq), 298.15 K)
= (1 mole)(-102.09 kJ/mole) – (2 mole)(0 kJ/mole) – (1 mole)(211.46 kJ/mole)
= -313.55 kJ
However, we can employ another route that illustrates the important method of thermodynamic cycles. Thermodynamics is not a subject such as quantum mechanics where molecular properties are calculated ab initio, i.e. from first principles. Rather, it is a subject that provides relations between quantities. These relations, if used properly, often enable one to convert available but seemingly uninformative information into useful results. Suppose that we have the standard enthalpy changes for the following processes: the gas-phase hydrogenation reaction (-311.41 kJ), dissolving ethane in water (-17.41 kJ/mole), and dissolving acetylene in water (-15.27 kJ/mole). The latter numbers might be provided by molecular modeling. We can use this information if we break up the net reaction into the following three steps:
Step I: HCºCH(aq) --> HCºCH(g) DH(I) = -(-15.27 kJ) [reverse!]
Step II: HCºCH(g) + 2 H2(g) --> C2H6(g) DH(II) = -311.41 kJ
Step III: C2H6(g) --> C2H6(aq) DH(III) = -17.41 kJ
Net: HCºCH(aq) + 2 H2(g) --> C2H6(aq) DH(net) = DH(I) + DH(II) + DH(III)
= -313.55 kJ
As before, the enthalpy changes of the individual steps add up to the enthalpy change for the net reaction because enthalpy is a state function. The overall enthalpy change did not change much but the enthalpy changes for the solvation steps are noteworthy. They are moderately large and negative even though other compelling evidence indicates that the solutes do not interact strongly with the solvent, water. It appears that something very interesting is going on. The late Henry Frank, Adjunct Professor of Chemistry at Pomona College, followed hints such as these and proposed the hydrophobic effect, a very important factor in the structure and properties of proteins.
REFERENCES AND RECOMMENDED READING
1.) H. A. Bent, The Second Law, Oxford, New York, 1965.
2.) N. C. Craig, Entropy Analysis, VCH, Weinheim, 1992.
Source: https://pages.pomona.edu/~wsteinmetz/handout/THERMO_1.DOC
Web site to visit: https://pages.pomona.edu
Author of the text: indicated on the source document of the above tex
THERMODYNAMICS
When a system is at equilibrium under a given set of conditions, it is said to be in a definite thermodynamic state. The state of the system can be described by a number of state quantities that do not depend on the process by which the system arrived at its state. They are called intensive variables or extensive variables according to how they change when the size of the system changes. The properties of the system can be described by an equation of state which specifies the relationship between these variables. State may be thought of as the instantaneous quantitative description of a system with a set number of variables held constant.
Several commonly studied thermodynamic processes are:
Adiabatic process: occurs without loss or gain of energy by heat
Isenthalpic process: occurs at a constant enthalpy
Isentropic process: a reversible adiabatic process, occurs at a constant entropy
Isobaric process: occurs at constant pressure
Isochoric process: occurs at constant volume (also called isometric/isovolumetric)
Isothermal process: occurs at a constant temperature
Steady state process: occurs without a change in the internal energy
An intensive property is a bulk property, meaning that it is a local physical property of a system that does not depend on the system size or the amount of material in the system. Examples of intensive properties include temperature, T; refractive index, n; density, ρ; and hardness of an object, η. By contrast, extensive properties such as the mass, volume and entropy of systems are additive for subsystems because they increase and decrease as they grow larger and smaller, respectively.
An intensive property is a physical quantity whose value does not depend on the amount of the substance for which it is measured. For example, the temperature of a system in thermal equilibrium is the same as the temperature of any part of it. If the system is divided by a wall that is permeable to heat or to matter, the temperature of each subsystem is identical; if a system divided by a wall that is impermeable to heat and to matter, then the subsystems can have different temperatures. Likewise for the density of a homogeneous system; if the system is divided in half, the extensive properties, such as the mass and the volume, are each divided in half, and the intensive property, the density, remains the same in each subsystem. Additionally, the boiling point of a substance is another example of an intensive property. For example, the boiling point of water is 100 °C at a pressure of one atmosphere, which remains true regardless of quantity.
The distinction between intensive and extensive properties has some theoretical uses. For example, in thermodynamics, the state of a simple compressible system is completely specified by two independent, intensive properties, along with one extensive property, such as mass. Other intensive properties are derived from those two intensive variables.
Examples of intensive properties include:
An extensive property is a physical quantity whose value is proportional to the size of the system it describes, or to the quantity of matter in the system. For example, the mass of a sample is an extensive quantity; it depends on the amount of substance. The related intensive quantity is the density which is independent of the amount. The density of water is approximately 1g/mL whether you consider a drop of water or a swimming pool, but the mass is different in the two cases.
Dividing one extensive property by another extensive property generally gives an intensive value—for example: mass (extensive) divided by volume (extensive) gives density (intensive).
State functions represent quantities or properties of a thermodynamic system, while non-state functions represent a process during which the state functions change. For example, the state function PV is proportional to the internal energy of an ideal gas, but the work W is the amount of energy transferred as the system performs work. Internal energy is identifiable; it is a particular form of energy. Work is the amount of energy that has changed its form or location.
The following are considered to be state functions in thermodynamics:
|
|
In the equation, the integrand can be expressed as the exact differential of the function P(t)V(t). Therefore, the integral can be expressed as the difference in the value of P(t)V(t) at the end points of the integration. The product PV is therefore a state function of the system.
The notation d will be used for an exact differential. In other words, the integral of dΦ will be equal to Φ(t1) − Φ(t0). The symbol δ will be reserved for an inexact differential, which cannot be integrated without full knowledge of the path. For example, δW = PdV will be used to denote an infinitesimal increment of work.
A quantity that is well defined so as to describe the path of a process through the equilibrium state space of a thermodynamic system is termed a process function,[1] or, alternatively, a process quantity, or a path function. As an example, mechanical work and heat are process functions because they describe quantitatively the transition between equilibrium states of a thermodynamic system.
Path functions depend on the path taken to reach one state from another. Different routes give different quantities. Examples of path functions include work, heat and arc length. In contrast to path functions, state functions are independent of the path taken.
The study of thermodynamical systems has developed into several related branches, each using a different fundamental model as a theoretical or experimental basis, or applying the principles to varying types of systems.
Classical thermodynamics is the description of the states of thermodynamic systems at near-equilibrium, that uses macroscopic, measurable properties. It is used to model exchanges of energy, work and heat based on the laws of thermodynamics. The qualifier classical reflects the fact that it represents the first level of understanding of the subject as it developed in the 19th century and describes the changes of a system in terms of macroscopic empirical (large scale, and measurable) parameters. A microscopic interpretation of these concepts was later provided by the development of statistical mechanics.
Statistical mechanics, also called statistical thermodynamics, emerged with the development of atomic and molecular theories in the late 19th century and early 20th century, and supplemented classical thermodynamics with an interpretation of the microscopic interactions between individual particles or quantum-mechanical states. This field relates the microscopic properties of individual atoms and molecules to the macroscopic, bulk properties of materials that can be observed on the human scale, thereby explaining classical thermodynamics as a natural result of statistics, classical mechanics, and quantum theory at the microscopic level.
Chemical thermodynamics is the study of the interrelation of energy with chemical reactions or with a physical change of state within the confines of the laws of thermodynamics.
Equilibrium thermodynamics is the study of transfers of matter and energy in systems or bodies that, by agencies in their surroundings, can be driven from one state of thermodynamic equilibrium to another. The term 'thermodynamic equilibrium' indicates a state of balance, in which all macroscopic flows are zero; in the case of the simplest systems or bodies, their intensive properties are homogeneous, and their pressures are perpendicular to their boundaries. In an equilibrium state there are no unbalanced potentials, or driving forces, between macroscopically distinct parts of the system. A central aim in equilibrium thermodynamics is: given a system in a well-defined initial equilibrium state, and given its surroundings, and given its constitutive walls, to calculate what will be the final equilibrium state of the system after a specified thermodynamic operation has changed its walls or surroundings.
Non-equilibrium thermodynamics is a branch of thermodynamics that deals with systems that are not in thermodynamic equilibrium. Most systems found in nature are not in thermodynamic equilibrium because they are not in stationary states, and are continuously and discontinuously subject to flux of matter and energy to and from other systems. The thermodynamic study of non-equilibrium systems requires more general concepts than are dealt with by equilibrium thermodynamics. Many natural systems still today remain beyond the scope of currently known macroscopic thermodynamic methods.
Those reactions in which heat is absorbed are called endothermic reactions.
e.g., N2(g)+O2(g)→2NO(g)−180.7kJ
Energy is being given in this reaction, therefore, it is an endothermic reaction
Those reactions which are accompanied by the evolution of heat are known as exothermic reactions.
C(s)+O2(g)→CO2(g)ΔH=−393.5kJ
Change in enthalpy is negative. Heat is released in this reaction, therefore, it is an exothermic reaction.
One definition of energy is the capacity to do work. There are many kinds of work, including mechanical work, electrical work, and work against a gravitational or a magnetic field. Here we will consider only mechanical work and focus on the work done during changes in the pressure or the volume of a gas.
Types of work:
Consider an ideal gas confined in a cylinder with a frictionless piston. The reversible expansion of gas takes place in a finite number of infinitesimally small intermediate steps. If the Pext is infinitesimally less than internal pressure of gas P by dP. Then gas expands reversibly and piston moves through a distance dl. Since dP is so small, for all practical purposes. Pext−Pgas=P
One work done by gas in one infinitesimal step (dw) can be expressed as; dw = PdV
If the gas expands from V1 to V2 during isothermal reversible expansion. The total amount of work done would be equal to
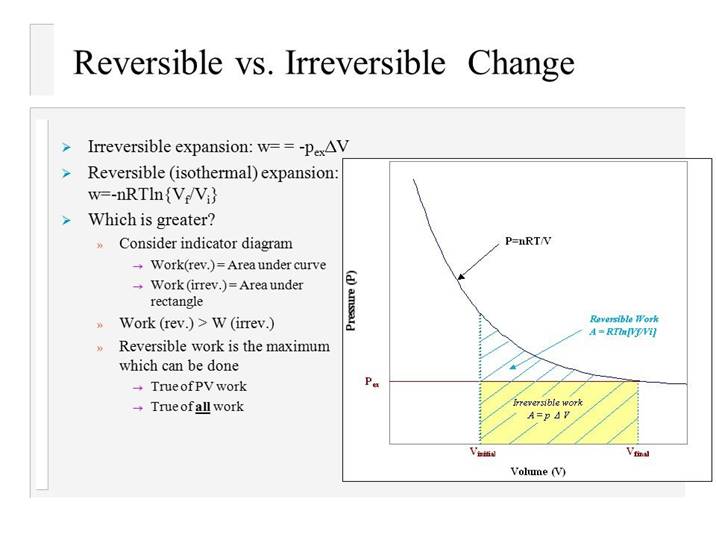
In irreversible expansion, the external pressure remains constant but in reversible expansion, external pressure has to be decreased continuously so as to remain infinitesimally smaller than the internal pressure.
Wrev>Wirr
It is mode of energy exchanged between the system and the surroundings as a result of the difference of temperature between them. It is usually represented by the letter q. When the heat is given by the system to the surroundings, it is given a negative sign. When the heat is absorbed by the system from the surroundings, it is given a positive sign. Units of heat are calorie, joule.
1 cal = 4.2 J
The maximum work that the system can do on the surroundings in an isothermal expansion of an ideal gas is obtained if the expansion is carried out reversibly.
An expression for the maximum work obtainable from the isothermal reversible expansion of a gas obeying the van der Waals equation of state, Using your expression, calculate how much work is done by one mole of carbon dioxide gas at a temperature T = 300.0K expanding from V_i = 10.00
Work is the quantity of energy transferred from one system to another without an accompanying transfer of entropy.
Thermodynamics is principally based on a set of four laws which are universally valid when applied to systems that fall within the constraints implied by each. In the various theoretical descriptions of thermodynamics these laws may be expressed in seemingly differing forms, but the most prominent formulations are the following.
This statement implies that thermal equilibrium is an equivalence relation on the set of thermodynamic systems under consideration. Systems are said to be in equilibrium if the small, random exchanges between them (e.g. Brownian motion) do not lead to a net change in energy. This law is tacitly assumed in every measurement of temperature. Thus, if one seeks to decide whether two bodies are at the same temperature, it is not necessary to bring them into contact and measure any changes of their observable properties in time.[25] The law provides an empirical definition of temperature, and justification for the construction of practical thermometers.
The zeroth law was not initially recognized as a separate law of thermodynamics, as its basis in thermodynamical equilibrium was implied in the other laws. The first, second, and third laws had been explicitly stated already, and found common acceptance in the physics community before the importance of the zeroth law for the definition of temperature was realized. As it was impractical to renumber the other laws, it was named the zeroth law.
The first law of thermodynamics states: In a process without transfer of matter, the change in internal energy, ΔU, of a thermodynamic system is equal to the energy gained as heat, Q, less the thermodynamic work, W, done by the system on its surroundings.
For processes that include transfer of matter, a further statement is needed: With due account of the respective fiducial reference states of the systems, when two systems, which may be of different chemical compositions, initially separated only by an impermeable wall, and otherwise isolated, are combined into a new system by the thermodynamic operation of removal of the wall, then
,
where U0 denotes the internal energy of the combined system, and U1 and U2 denote the internal energies of the respective separated systems.
Adapted for thermodynamics, this law is an expression of the principle of conservation of energy, which states that energy can be transformed (changed from one form to another), but cannot be created or destroyed.[27]
Internal energy is a principal property of the thermodynamic state, while heat and work are modes of energy transfer by which a process may change this state. A change of internal energy of a system may be achieved by any combination of heat added or removed and work performed on or by the system. As a function of state, the internal energy does not depend on the manner, or on the path through intermediate steps, by which the system arrived at its state.
Source: https://www.mlsu.ac.in/econtents/2252_Thermodynamics-Introduction.docx
Web site to visit: https://www.mlsu.ac.in
Author of the text: indicated on the source document of the above text
If you are the author of the text above and you not agree to share your knowledge for teaching, research, scholarship (for fair use as indicated in the United States copyrigh low) please send us an e-mail and we will remove your text quickly. Fair use is a limitation and exception to the exclusive right granted by copyright law to the author of a creative work. In United States copyright law, fair use is a doctrine that permits limited use of copyrighted material without acquiring permission from the rights holders. Examples of fair use include commentary, search engines, criticism, news reporting, research, teaching, library archiving and scholarship. It provides for the legal, unlicensed citation or incorporation of copyrighted material in another author's work under a four-factor balancing test. (source: http://en.wikipedia.org/wiki/Fair_use)
The information of medicine and health contained in the site are of a general nature and purpose which is purely informative and for this reason may not replace in any case, the council of a doctor or a qualified entity legally to the profession.
The texts are the property of their respective authors and we thank them for giving us the opportunity to share for free to students, teachers and users of the Web their texts will used only for illustrative educational and scientific purposes only.
All the information in our site are given for nonprofit educational purposes