Vacuum

PART I. VACUUM METODS

1. VACUUM FUNDAMENTALS

High vacuum = low pressure of gas

 

Physical problems in vacuum techniques = physics of gases, classical approximation (no quantum effects). Molecular kinetic gas model.

Applications of vacuum in the experiments:

1. thermal and/or acoustic isolation
2. environment separation, no collisions (accelerators, particle physics), clean surfaces, non-contaminating environment for technological processes, crystal growth, diffusion, film growth

 Physics of gases: Free and Bounded (on the surface and in the volume) gas. Vacuum problems – classical kinetic molecular gas models. No quantum effects. Gas molecules behave like elastic mechanical particles moving due to thermal energy.

Free gas

Remember:
Avogadro number: NA = M0/m0 = 6.1023 mol-1;
M0 = molecular mass,  m0 = mass of a molecule

Mean free path:

Thermal energy and moving gas particles:
(1)     

where the value of  is depended on the choice of v:
v=vvpr   the most probable velocity, c1=k=1.38 10-16 erg/K  
v=var arithmetical  average  velocity,  c1=(4/p)k
v=v2av  mean square velocity,  c1=(3/2)k

Example: nitrogen molecules @ 300 K:
vvpr   = 400 m/s  
var = 450 m/s
v2av  = 490 m/s
The mean free path () is proportional to:
(2)        [cm],   
n1 - concentration of gas molecules cm-3 ,  d-diameter of the molecule [cm]
Example: the mean free path of air (Ar, N2, O2 ; d~3.7 10-8 cm) @300K.:
Table1:  mean free path for air (T»300k)

	760	1	10-3	10-9
	2.5*1018	3.3*1015	3.3*1013	3.3*107
	6.6*10-5	0.05	5	5*106

1.1.3. Pressure.

The frequency of collision of gas molecules with the wallis proportional to concentration and velocity:
(3)    
when f1 [s-1cm-2],  n1 [cm-3],  v=vav   then : c3 = 0.25

The momentum transfer at an elastic collision with the wall:  m0v-(-m0v)=2m0v.
The force on a unit surface (pressure) pressure is:

(4)   

where is a proportionality constant that depends on the choice of pressure units and the definition of the velocity.

1.1.3.1. Pressure units

• Torr, 1Tr  = 1 mm Hg
• Physical atmosphere, normal atmosphere, 1 Atm  =  760 Torr
• Technical atmosphere, 1 At = 1Kg/cm2
• Pascal; 1 Pa  = 1 N/m2  = 1.02 *10-5 At =0.99 Atm=0.75*10-2 Torr
• 1 bar  = 103 mbar = 7.5*102 Torr =105 Pa = 1 Hectopascal
• 1 mbar = 0.75 Torr
• 1 PSI  = 1pound/inch2

conversion table: to be inserted

1.1.3.2. Relation between pressure, concentration, and temperature.

 Express m0v2 as a function of T . From  (4)  we have  and since   we get
(5)    
when T [K],  p [Tr],  n1 [cm-3]   then: =10-5   and:

 (6)     

From (5) we can get for the concentration:
(7)     
For Air (d~3.7 10-8 cm) l0  ~ 1.6 T [K] / p [Tr] . At room temperature l0 (300K) = 5*10-3 / p [Tr].

N.B. In a closed container a temperature change will not change l0 since  simultaneously the pressure is changing.

1.1.4. Properties of the Air

Table 2: Air - components

	% vol.’	% weight	p[Tr]
N2	78	75.5	590
O2	20.95	23.14	160
Ar	0.93	1.25	7
CO2	0.03	0.05	0.25
Ne	0.002	0.001	0.014
He	52*10-4	72*10-5	4*10-3
H2	5*10-5	5*10-6	4*10-4

Air pressure changes with altitude.

Table 3: atmospheric pressure vs. altitude

Alt.[km]	0	14	30	47	78	100	200	480
p[Tr]	760	100	10	1	10-2	10-4	10-6	10-8

In between the sea level and about 14 km pressure changes almost linearly with the altitude. 
For calibration of pressure meters an absolute meter is needed as a reference.

1.1.5. Vacuum ranges

 

Vacuum classes corresponding pressure ranges
Forvacuum   (technical)              p>10-3
Low vacuum  (LV)              10-3>p>10-6
High vacuum  (HV)           10-6>p>10-9
Ultra high vacuum (UHV)  10-9>p>10-12
Extremely high vacuum              p<10-12

“Clean” and  “dirty” vacuum: possible contaminations water, oil, specific contaminations, helium, noble gases, hydrogen.

1.1.6. Amount of gas and the state equation of gas

The product Q=pV is referred to as an the amount of gas in pV units [Tr*l], [Pa*m3], etc.

Boyle- Mariotte`s law (B-M law):
(8)     
,   ,   mass of a gas molecule
from  (5) we have :
(9)          ,
and we obtain the B-M law for the amount of gas (Q):
(10)          
Introducing the universal gas constant
(11)          .
Expressing m in [g], M0 in [g/mol], T in [K], p in [Tr], and V in [l] R=62.37.
In other units R=8.32 104 J/(mol *K), etc.

1.1.7. Flow of gas, intensity and velocity of flow

 

Intensity of flow is defined as an amout of gas (Q) flowing in a unit time by a cross-section perpendicular to the direction of the flow:
(12)         

 Using B-M law we have:         (13)        
were n=nm0  stands for the number of gas particles.
The velocity of flow S is defined as:  
Units of S; [m3/h], [l/s]. etc.

• When S<0 we have the pumping effect
• When S>0 we have leak or degassing effect.

 

(14)     
From  (14) we get the relation        (16)       

1.1.8. Intensity and velocity of pumping by an ideal pump

Consider an opening leading to an ideal vacuum (ideal pump).  The factor which determines the escape intensity (pumping intensity) is the number of collusion with the opening per unit time,
Using 3 and 13 we get for the intensity:
(17)    
f’- number of gas particles hitting a unit surface in a unit time, p – pressure in the pumped volume.
Using  (16) we obtain the velocity of flow through an opening of  an area A:
(18)     
Observe that the velocity of flow (pumping speed) decreases with increasing mass of gas molecules, temperature and evidently is proportional to the surface of the opening.
Example: @300° K   SA  for Air (m0~ 5*10-25 g) = 11.7 A,  while for H2  (m0~ 3.4*10-24 g ) SA » 45A .

 

1.1.9. Change of pressure at a constant velocity of flow.

Consider a container of a constant volume V that is connected to a pump with a constant pumping speed S. How pressure in the container changes in time?
From  (13 )    , and,  on the other hand  , therefore

and since number of particles is proportional to the pressure we can write

(19)          

Thus pressure exponentially drops to zero with elapsing time. In the experimental reality we do not have an ideal vacuum. There is some finite limiting minimum pressure p¥  available with a particular pump:

 (20)   

 

 

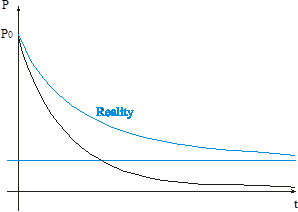
Consider an inverse process. We pump down, and after a time t stop pumping:

 

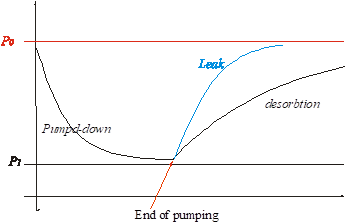                                 p

 

This can be employed to check for leaks in the system.

1.1.10 Flow of gas through tubes

 
There are three distinct regimes of flow in tubes.

1.1.10.1. Molecular flow

In this regime the free path of the gas is longer than the diameter of the tube. Each particule behaves individually. There are almost no  collisions between the molecules. Thy collide mostly with the walls of the tube. After a collision the particle velocity direction is random and therefore part of the molecules is “back-scattered” towards the input. In this case the effective mean free path is

, where D is the diameter of the tube.

 

For air we have molecular flow for

1.1.10.2. Laminar flow

Most of the collisions are between the molecules. The flow has a velocity distribution with the maximum in the center of a tube.
 

 

For air .

The flow is laminar as long as     
Laminar flow is characterized by low Reynolds number.

1.1.10.3. Turbulent flow

 

 

 

1.1.11. Resistance for gas flow

Speed of pumping of an ideal pump (opening to an ideal vacuum) is given by (18). However, when the opening is connected to the pumped volume by a tube the pumping speed is reduced due to a resistance to the gas flow in the tube. This is due to a friction resulting from collision of molecules with the walls and between themselves.

Molecular conditions

The  longer and the narrower is the tube, more collisions, the higher is the resistance for the flow W.

Tube resistance W follows from the difference in flow velocities
.
Note that only for when   and W=0.
Usually one defines the conductivity of a tube, , units of G: [l/s]

For a cylindrical tube with L>5D one can use the following approximation:

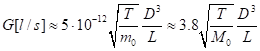   (D and L in cm)

For air @300K  
.
Example: A circular tube with D=1cm and L=10cm has a conductivity of G=1.22l/s for Air at 300K. If this tube is connected to the opening of the same diameter leading to the ideal vacuum the speed of pumping of the opening will be S=9l/s. The speed of pumping at the tube inlet will be however:

N.B. Even such a short  tube reduces the speed of pumping from 9 l/s to 1.1 l/s! Proper design of vacuum systems and pumps: short and wide tubes (large apertures create however other problems).

For an opening: the velocity of escape through an opening = the aperture (hole) conductivity G0=1/W0 Since the impedance of  a hole is not zero, in general, the resistance of a tube is:

  , thus even for  ,

1.1.11.1. Connecting tubes

 
Similarly to electrical circuits:

  for a serial connection, and

  for a parallel connection.

 

1.1.11.2 Pumping speed at the other end of a tube.

S- pumping speed, G- tube conductivity and the  pumping speed at the other end of a tube

,

Therefore, for  G>>S the pumping speed S=S` and is not reduced by the tube. However, when  G<<S then S`=G and the pumping speed is limited not by the pump used but by the piping. Always adjust pump to the tube and/or the tube to the pump.

1.2. Surface bounded gas

1.2.1 Desorption

                                               p(d)

 

Gas molecule departing from the surface. Angular distribution of  velocities of desorbing molecules.

 

The time of permanence on the surface:

is the time it takes for a molecule to detach itself from the surface (desorption).  is the temperature of the surface,  and  depends on the molecule and the surface. For higher surface temperature the time for detachment decreases.

In free and clean surface the first layer of gas molecules is bonded by metallic bonds (exchanging of electrons). Next  layers are attached by atomic (covalent) bonds (deformation of electrons orbitals).

Noble gases – van der Waals bonds – weaker bonds “physical bonds”
Bonding energies () in kcal/mole for a clean W surface

He	Kr	H	CO2	O	O2	N2	N
2	4.5	74	122	147	194	85	155

1.2.2. Absorption

 

Permanent permanence of the gas molecule on the surface. In the act of absorbtion a latent heat of absorbtion is released and the gas particle remains bounded. For this reason it is hard to absorb noble gases – low energy of bonding.

1.2.2.1. Attachment coefficient and the degree of covering the surface

The frequency at which gas molecules are hitting the surface is

,

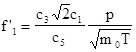but only a fraction of those hits are effective (in a sense of attachment to the surface),  , where  is the attachment coefficient.

The degree of covering is , where N is the number of particles located on the surface,  is the number of the available sites on the surface. With increasing ,  decreases. The absorption speed depends on p, T, and the surface state through the coefficient g.

The time of total surface covering

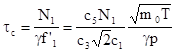
For air @ 300K and for =0.5,    , meaning that

• t [10-6 Tr] ~ 1 second
• t [10-9 Tr] ~ 1 hour
• t [10-12 Tr] ~ 1 month

1.2.3 Surface and vacuum

 

• Good vacuum needs clean surfaces – mechanical, chemical, ion, and  thermal cleaning
• Surface analysis – possible only in the UHV vacuum conditions

The intensity and velocity of  adsorption / desorption from the surface A exposed to an ideal vacuum

The velocity of  adsorption/desorption .
For air at 300K, .
The effective absorption frequency was given in the previous section. For the desorption frequency

, where N is the number of molecules on the surface.
In equilibrium , and we can solve for N:

1.2.3. Evaporation and condensation

 

Equilibrium vapour pressure above a surface of a material is

insert graph of the vapour pressure vs  temperature for various materials.

Insert table of melting and  boiling temperatures of various elements.

1.2.4. Materials for vacuum systems

MOOV
1H13N9T and 1H13

1.3.  Gas in the Solid State

1.3.1. Solubility of gas in metal and glass

Noble gases: Henry`s low: , where  is the quantity of gas in pV units referred to 760 Tr and 1cm3.

Diatomic gases:  Sieverst’s low :
Notice that solubility coefficients  and  have different units.  These coefficients are temperature dependent. In general  increase with temperature,  stronger for metals than for glass.

For glasses: r1 ~0.005 – 0.01 in the temperature range  (20-400o C)
For metals:  r2 ~ 0.001- 1 in the temperature range  (200-1000o C)

The dissolved gas moves in solids by diffusion:

.

1.3.2. Penetration through the walls

 

The amounts of gas that penetrates through 1cm2 along the distance L in 1s is:

The permeability coefficient is defined as:

,

 

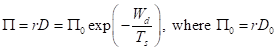insert graph and 2 tables

 

General requirement for vacuum materials: low permeability!