Relational database design

UNIT-3 RELATIONAL DATABASE DESIGN

PITFALLS IN DATABASE DESIGN

• Redundant  information in tuples
• Update anomalies

REDUNDANT INFORMATION IN TUPLE:
One goal of schema design is to minimize the storage space that the base relations occupy. Grouping attributes into relation schemas has a significant effect on the storage.
For (eg), compare the space used by the two base relations EMPLOYEE and DEPARTMENT with EMP_DEPT base relation which is the result of applying the NATURAL JOIN operation to EMPLOYEE and DEPARTMENT.
In EMP_DEPT, the attribute values pertaining to a particular department are repeated for every employee who works for that department.
In contrast, each department’s information appears once in DEPARTMENT relation.
i.e, EMP_DEPT-(ename, eid, DOB, Address, dno, dname, dMGRid)

UPDATE ANOMALIES:
Types

• insertion anomalies
• Deletion anomalies
• Modification anomalies

i) Insertion anomalies: These can be differentiated into two types

• To insert a new employee tuple into EMP_DEPT, we must include the attribute values for the department that the employee works for, or nulls (if the employee does not work for a department as yet).
• It is a difficult to insert a new department that has no employee as yet in EMP_DEPT relation. The only way is to place null values in the attributes for employee. This causes a problem because eid is a primary of EMP_DEPT.

ii) Deletion anomalies: If we delete for EMP_DEPT an employee tuple that happens to represents the last employee working for a particular department, the information concerning that department is lost from the database.

iii) Modification anomalies: In EMP_DEPT, if we change the value of one of the attributes of a particular department, say the manager of department 10 we must update the tuples of all employees work in that department. Otherwise the database will become inconsistent.

FUNCTIONAL DEPENDENCIES
Functional dependencies play a key role in differentiating good database design from bad database designs. A functional dependency is a type of constraint that is a generalization of the notation of key.

Definition:
A functional dependency is denoted is denoted by X→Y, between two sets of attribute X and Y that are subsets of R specifies a constraint on the possible tuples that can form a relation state r of R.
The constraint is that, for any two tuples t1 and t2 in r that have t1[X] = t2[X] also t1[Y] = t2[Y].
This means that the values of the Y component of a tuple in r depends on, or are determined by, the values of the X component.
The values of the X component of a tuple uniquely (or functionally) determine the values of the Y component. Y is functionally dependent on X.
EMP-PROJ= {eid, pnumber, hours, ename, pname, plocation}
Eg., Consider the relation schema EMP-PROJ from the semantics of the attributes.
The following functional dependencies should hold.

• Eidèename
• Pnumberè{pname, plocation}
• {eid, pnumber}èhours

Diagrammatic notation for displays FD’s

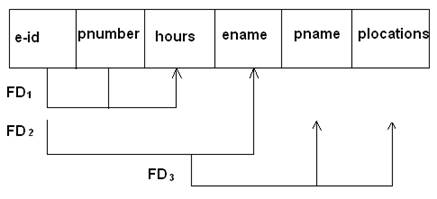
Each FD is displayed as a horizontal line. The LHS attributes of the FDs are connected by vertical lines to the lines representing FD, while the RHS attributes are connected by arrows pointing toward the attributes.

INFERENCE RULES FOR FUNCTIONAL DEPENDENCIES
F is the set of functional dependencies that are specified on relation schema R. Numerous other FDs hold in all legal relation instance that satisfy the dependencies in F.
The set of all such dependencies are called closure of F and is denoted by F.
F= {Eid è {ename, dob, address, dno}
dno è{ dname, dMGRid }
We can infer the following additional FDs from F:
eid è {dname, dMGRid }
dno è dname, eid è eid
An FD XèY is inferred from a set of dependencies F specifies on R if XèY holds in every relation state r that is legal extension of R. (ie) whenever r satisfies all the dependencies in F, XèY also holds in r.
The closure F+ of F is the set of all FDs that can be inferred from F. Inference rules that can be used to infer new dependencies from a given set of dependencies.
IR1 (reflexive rule): If X  Y then X èY.
IR2 (Augmentation rule): {XèY} ≠ XZ èYZ
IR3 (Transitive rule): {XèY, YèZ} ≠XèZ
IR4 (Decomposition (or) Projective Rule):  {XèYZ} ≠ XèY
IR5 (Union or Additive rule): {XèY, XèZ} ≠ XèYZ
IR6 (Pseudo Transitive Rule): {XèY, WYèZ} ≠ WXèZ

• IR1 states that a set of attributes always determines itself or any of its subsets. Because IR1 generates dependencies that are always true. Such dependencies are called trivial.
• IR2 says that adding same set of attributes to both LHS and RHS of a dependency results another valid dependency.
• IR4 we can remove attributes from RHS.

            The inference rules IR1 through IR3 are known Armstrong’s Inference Rules (or) Armstrong’s Axioms. Thus for each set of attributes X, we determine the set X+ of attributes that are functionally determined by X based on F X+ is called the closure of X under F.

Algorithm: Calculate X+ (Closure of Attributes Sets)
X+ :=X;
Repeat
For each functional dependency x in X+ apply reflexivity and augmentation rules on x add the resulting functional dependencies to ‘X’.
For each pair of functional dependencies x1 and x2 can be combined using transitivity add the resulting functional dependency X+.
Until X+ does not change further.

CANONICAL COVER
An attribute of a functional dependency is said to be extraneous if we can remove it without changing the closure of the set of functional dependencies.
Definition: Consider a set F of functional dependencies and the functional dependency αèβ in F.

• Attribute A is extraneous in α if A € α, and F logically implies {F-{αèβ}} U {{α-A}èβ}.
• Attribute A is extraneous if β if A € β, and the set of functional dependencies

  {F - {α - β}} U {α {β – A}} logically implies F
A canonical cover Fc for F is a set of dependencies such that F logically implies all dependencies in Fc, and Fc logically implies all dependencies in F. Fc must have the following properties.

• No functional dependency in Fc contains an extraneous attribute.
• Each left side of functional dependency in Fc  is unique. (ie) there are no two dependencies α1èβ1 and α2èβ2 in  such that α1=α2.

(eg) Consider the following set F of functional dependencies on schema (A, B, C).
AèBC
BèC
AèB
ABèC
Compute the canonical cover for F.

• There are two functional dependencies with the same set of attributes on the left side of the arrow.

                                       AèBC
AèB
These FD;s will be combine into AèBC

• A is extraneous in ABèC because F logically implies {F==.{ AèBC}}U{ BèC). This assertion is true because BèC is already is our set of FDs.
• C is extraneous in AèBC, since AèBC is logically implied by AèB and BèC

Canonical cover is     AèB
BèC.

Dependency Preservation:
This property ensures that a constraint on the original relation can be maintained by simply enforcing some constraint on each of the smaller relations.

NORMALIZATION
Normalization of data is a process of analyzing the given relation schema based on their FDs and primary keys to archive the desirable properties of

• Minimizing redundancy
• Minimizing the insertion, deletion and update anomalies.

First Normal Form (1NF)
It states that the domain of an attribute must include only atomic (Simple, indivisible) values and that the value of any attribute in a tuple must be a single value from the domain of that attribute.

S#	S_NAME	S_ADDRESS	P#	P_NAME	P_CITY	P_STATUS	QTY
S001	HCL	NORTH STREET, CHENNAI	P001	MOUSE	DELHI	100	150
S002	IBM	WEST STREET, MADURAI	P001	MOUSE	MUMBAI	120	200
SOO2	IBM	WEST STREET, MADURAI	P002	KEY BOARD	PUNE	75	150
S003	DELL	SOUTH STREET, COIMBATORE	P003	HARD DISK	DELHI	100	180
S004	HCL	EAST STREET, TRICHY	P004	DVD DRIVE	PUNE	75	200

TABLE-A
In the table-A the supplier address contains street and city. 1NF states that the domain of an attribute must include only atomic (Simple, indivisible) values. So we have to split S_ADDRESS into S_STREET and S_CITY.

S#	S_NAME	S_STREET	S_CITY	P#	P_NAME	P_CITY	P_STATUS	QTY
S001	HCL	NORTH	CHENNAI	P001	MOUSE	DELHI	100	150
S002	IBM	WEST	MADURAI	P001	MOUSE	MUMBAI	120	200
S002	IBM	WEST	MADURAI	P002	KEY BOARD	PUNE	75	150
S003	DELL	SOUTH	COIMBATORE	P003	HARD DISK	DELHI	100	180
S004	HCL	EAST	TRICHY	P004	DVD DRIVE	PUNE	75	200

TABLE-B

SECOND NORMAL FORM (2NF)
A relation is said to be in the second normal form, if it is already in the first normal from and it has no partial dependency (or) full functional dependency.
In the above table B the key attributes are S# and P#. The non-key attributes must depend on key attribute. But the Table-B, S-NAME, S_STREET and S-CITY depend on S# and P_NAME, P_CITY and P_STATUS depends on P#. Only QTY depends on both key attributes S# and P#. So we have to split the table.

Join over parts

S#	P#	J#
S001	P001	J001
S001	P001	J002
S001	P002	J001
S002	P001	J001

                                                                                                                                   

 

 

                                                                  

 

 

 

Join Supplier_Product & Product_Project with Project_Supplier